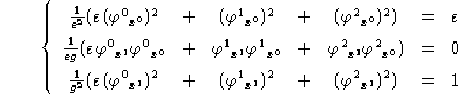
Il sistema 1.1 può essere riscritto, dato che e,g sono strettamente positivi, nella forma:
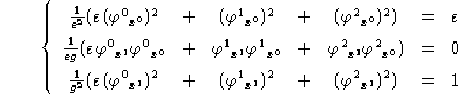
Manteniamo e non sostituendoci 1 perchè dato che capita spesso di
avere metriche già in forma diagonale, ci sono buone possibilità di poter
applicare direttamente i metodi risolutivi che illustreremo senza dover
prima diagonalizzare come illustrato nella sezione 1.2. La
prima equazione di questo sistema mi dice che il vettore
![]() , nel caso lorenziano (
, nel caso lorenziano ( ![]() ), identifica un punto,
che al variare di
), identifica un punto,
che al variare di ![]() , mi rimane sempre sulla superfice di un iperboloide
di equazione implicita
, mi rimane sempre sulla superfice di un iperboloide
di equazione implicita ![]() . Nel caso riemanniano
(
. Nel caso riemanniano
( ![]() ) il punto identificato da
) il punto identificato da ![]() mi rimane su una
sfera di raggio unitario e di equazione
mi rimane su una
sfera di raggio unitario e di equazione ![]() .
.
Analogo discorso per la terza equazione ed il vettore ![]() .
La seconda equazione mi dice semplicemente che i due vettori
.
La seconda equazione mi dice semplicemente che i due vettori
![]() e
e ![]() sono perpendicolari fra di
loro (in
sono perpendicolari fra di
loro (in ![]() con il prodotto scalare relativo) per ogni
con il prodotto scalare relativo) per ogni ![]() contenuto
nel dominio di definizione
contenuto
nel dominio di definizione ![]() di
di ![]() ,
, ![]() ,
, ![]() .
.
Quanto detto deve valere per qualunque possibile soluzione ![]() del
sistema 1.1 definita su
del
sistema 1.1 definita su ![]() . Queste considerazioni ci
suggeriscono una riformulazione di carattere vettoriale:
. Queste considerazioni ci
suggeriscono una riformulazione di carattere vettoriale:
Teorema
1.33
[di Equivalenza]
Data una metrica definita sul rettangolo di
dalla matrice:
con
che soddisfano
con:
Allora esiste una soluzione:
del sistema:
ed è data da:
con fissati a piacere
Viceversa se ![]() :
:
![]()
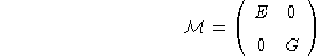
![]() ,
, ![]() ; Se esistono due applicazioni
; Se esistono due applicazioni
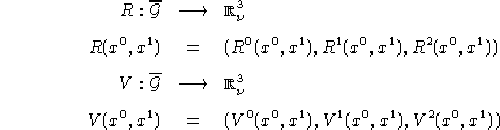
![]() :
:
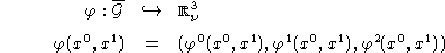
![]() ,
, ![]() e
e
![]() .
.
![]() soddisfa il sistema 1.5 ed ha
derivate seconde continue, allora le due funzioni:
soddisfa il sistema 1.5 ed ha
derivate seconde continue, allora le due funzioni:
![]()
Dimostrazione
![]() ) Le forme:
) Le forme:
![]()
risultano essere chiuse per la condizione imposta sulle derivate parziali
di R e V dall'eq. 1.4 delle ipotesi. Dato che siamo in
un dominio rettangolare, che è in particolare un dominio stellato, le
forme ![]() oltre che chiuse sono anche esatte e quindi ha senso
definire:
oltre che chiuse sono anche esatte e quindi ha senso
definire:
![]()
con le costanti ![]() ,
, ![]() ,
, ![]() scelte a piacere e naturalmente vale
scelte a piacere e naturalmente vale ![]() , ovvero:
, ovvero:

Esaminando le tre equazioni del sistema e tenendo conto che valgono le equazioni 1.3 e le 1.4 si ottiene:
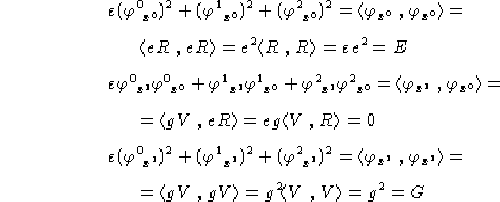
Quindi il sistema è risolto da ![]() come definita sopra.
come definita sopra.
![]() ) Viceversa se
) Viceversa se ![]() soddisfa il sistema 1.5 ed ha
derivate continue, allora definiamo le funzioni
soddisfa il sistema 1.5 ed ha
derivate continue, allora definiamo le funzioni ![]() ,
, ![]() come:
come:
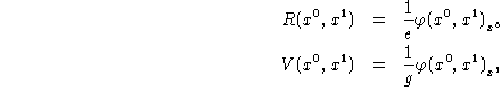
È immediato verificare che R,V soddisfano le equazioni 1.3
del teorema dato che ![]() soddisfa per ipotesi il sistema
1.5, per quanto riguarda la seconda richiesta sulle funzioni
R,V data dall'equazione 1.4 delle ipotesi, osserviamo:
soddisfa per ipotesi il sistema
1.5, per quanto riguarda la seconda richiesta sulle funzioni
R,V data dall'equazione 1.4 delle ipotesi, osserviamo:

Ma dato che per ipotesi ![]() ha derivate seconde continue segue che
vale:
ha derivate seconde continue segue che
vale:
![]()
e quindi R,V definiti precedentemente soddisfano anche l'equazione 1.4 delle ipotesi.
![]()
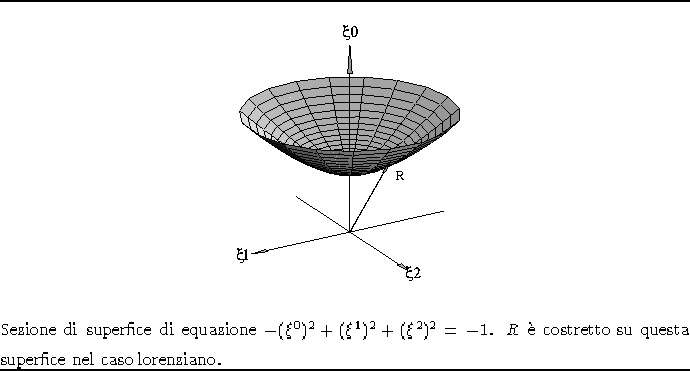
Figura 1.7: Ramo di iperboloide.
Una delle condizioni per poter applicare il teorema di equivalenza, è che deve valere nel caso lorenziano:
![]()
Affinchè ciò sia vero, R deve variare sulla superfice di un iperboloide
di equazione ![]() , e dato che R deve essere
continua, segue che i possibili valori di R sono confinati sulla
superfice di un'unico ramo dell'iperboloide (fig. 1.7).
, e dato che R deve essere
continua, segue che i possibili valori di R sono confinati sulla
superfice di un'unico ramo dell'iperboloide (fig. 1.7).
Avendo R arbitrario sappiamo, se vogliamo che l'eq. 1.3 del Th. di Equivalenza siano verificate, che V dovrà stare su un piano perpendicolare ad R, e variare, nel caso lorenziano, su un ramo di iperboloide di equazione:
![]()
tipo quello di fig. 1.8.
Nel caso riemanniano R e V dovranno soddisfare rispettivamente:
![]()
![]()
e quindi sono confinati a variare su una sfera tipo quella di fig. 1.9, 1.10.
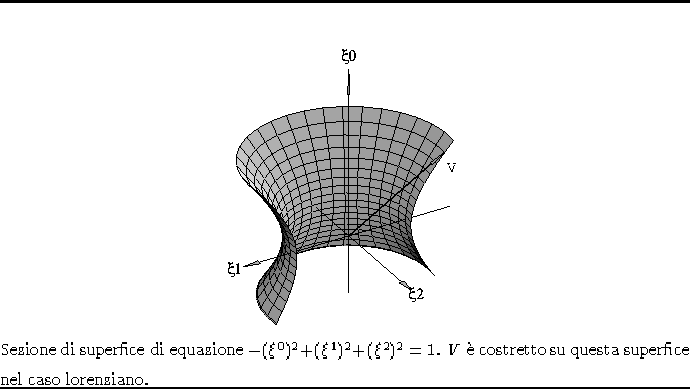
Figura 1.8: Ramo cilindrico di iperboloide.
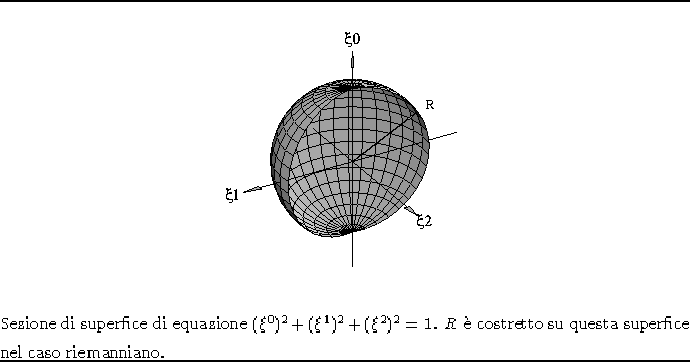
Figura 1.9: Sfera unitaria per R.
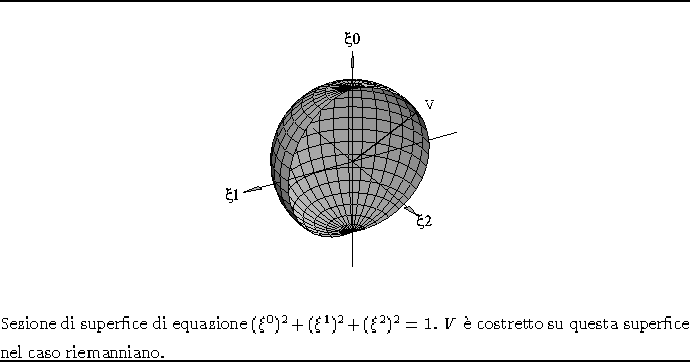
Figura 1.10: Sfera unitaria per V.
Queste considerazioni ci suggeriscono la definizione seguente:
Definizione
1.34
Facendo riferimento alla figura 1.11, fissato un vettore R
e un vettore V giacente su un piano perpendicolare a R, definiamo:
![]() è l'angolo tra il vettore R e l'asse
è l'angolo tra il vettore R e l'asse ![]() .
.
![]() è l'angolo tra l'asse
è l'angolo tra l'asse ![]() e la proiezione P sul
piano
e la proiezione P sul
piano ![]() del vettore R.
del vettore R.
![]() perpendicolare al vettore R e passante per
l'origine. Contiene V.
perpendicolare al vettore R e passante per
l'origine. Contiene V.
![]() passante per
passante per ![]() e R.
e R.
![]() e il piano
e il piano ![]() e di direzione opposta a p.
e di direzione opposta a p.
![]() tra il vettore Q e il vettore V.
tra il vettore Q e il vettore V.
Ricordando le relazioni trigonometriche e trigonometriche iperboliche fondamentali:
enunciamo:
Proposizione
1.35
Siano
===
===
e V uguale a:
===
===
allora valgono, qualunque sia il valore assunto da
![]() funzioni arbitrarie a valori in
funzioni arbitrarie a valori in ![]() .
Ponendo R uguale a:
.
Ponendo R uguale a:
![]()
![]()
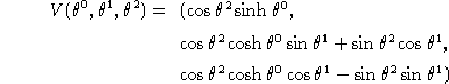
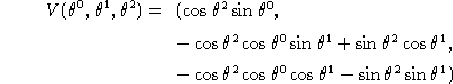
![]() , le equazioni
1.3 del Teorema di Equivalenza, ovvero:
, le equazioni
1.3 del Teorema di Equivalenza, ovvero:
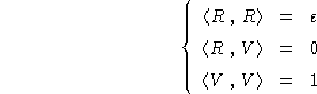
La dimostrazione si potrebbe effettuare brutalmente calcolando i prodotti scalari e sostituendo le espressioni di R e V nei due casi, tenendo conto che valgono le relazioni 1.7. L'inconveniente di questo tipo di dimostrazione è che mentre per R è evidente come è stato ottenuto (non è altro che la parametrizzazione di un ramo di iperboloide o di una sfera), per V non è altrettanto evidente. Per questo adotteremo una dimostrazione di tipo costruttivo per V mentre per R ci limiteremo a fare delle semplici verifiche.
Dimostrazione Verifichiamo la validità dell'espressione di R nel caso lorenziano:
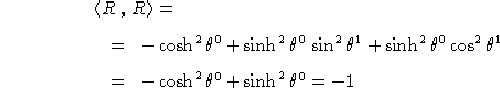
e nel caso riemanniano:
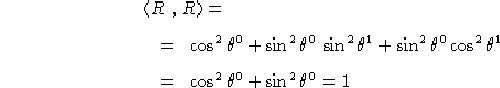
Esaminiamo ora V. Deve valere, riportando come al solito in caratteri di dimensioni inferiori il caso riemanniano:
![]()
===
![]()
=== quindi V deve variare su un ramo di iperbolide (sfera) tipo quello di fig. 1.8 (fig. 1.9) analogamente a quanto deve fare R, con in più la condizione che V deve essere perpendicolare a R.
Prendendo la definizione 1.34 per i ![]() , e tenendo
presente la figura 1.12 mostriamo come si possa ricavare
l'espressione di V. Il caso lorenziano è del tutto simile al caso
riemanniano quindi riporteremo le differenze, ove presenti, tra parentesi o
in caratteri tipografici di dimensioni inferiori.
, e tenendo
presente la figura 1.12 mostriamo come si possa ricavare
l'espressione di V. Il caso lorenziano è del tutto simile al caso
riemanniano quindi riporteremo le differenze, ove presenti, tra parentesi o
in caratteri tipografici di dimensioni inferiori.
Divido V come somma delle proiezioni lungo la retta del vettore
![]()
![]() e la retta di intersezione tra i piani
e la retta di intersezione tra i piani ![]() e
e ![]() che sarà lungo
il vettore
che sarà lungo
il vettore ![]() . Indicando con
. Indicando con ![]() il vettore unitario
lungo tale retta e con verso uguale a W. Vale:
il vettore unitario
lungo tale retta e con verso uguale a W. Vale:
![]()
![]() ha solo componenti lungo
ha solo componenti lungo ![]() e
e ![]() , e dato che la proiezione
di
, e dato che la proiezione
di ![]() su
su ![]() è pari a
è pari a ![]() (
( ![]() ), si ha:
), si ha:
![]()
===
![]()
===
La proiezione di ![]() sul piano
sul piano ![]() ha modulo pari a
ha modulo pari a ![]() (
( ![]() ) che ha componenti:
) che ha componenti:

===

===
mentre le componenti di ![]() sono:
sono:

sostituendo nell'espressione di V:
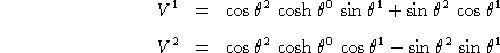
===
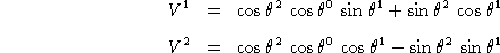
===
![]()
Osservazione
1.36
Per soddisfare le condizioni 1.3, pg. ![]() del Teorema di Equivalenza
non abbiamo dovuto imporre nessuna restrizione sulle
del Teorema di Equivalenza
non abbiamo dovuto imporre nessuna restrizione sulle ![]() dato che le
1.3, pg.
dato che le
1.3, pg. ![]() vengono soddisfatte automaticamente per qualunque valore
assunto dalle
vengono soddisfatte automaticamente per qualunque valore
assunto dalle ![]() se R e V sono nella forma data dalla precedente
proposizione 1.35.
se R e V sono nella forma data dalla precedente
proposizione 1.35. ![]()
Ora l'unica altra condizione che dobbiamo soddisfare per poter applicare il
Th. di Equivalenza è trovare degli opportuni ![]() funzioni di
funzioni di ![]() affinchè si verifichi:
affinchè si verifichi:
![]()
con R e V nella forma data nella precedente proposizione
1.35 e ![]() funzioni dipendenti in maniera derivabile da
funzioni dipendenti in maniera derivabile da
![]() a valori in
a valori in ![]() . Questa condizione mi imporrà delle equazioni che
dovranno essere soddisfatte dalle
. Questa condizione mi imporrà delle equazioni che
dovranno essere soddisfatte dalle ![]() affinchè
possa essere applicato il Teorema di Equivalenza per trovare l'immersione.
affinchè
possa essere applicato il Teorema di Equivalenza per trovare l'immersione.
Questo problema verrà trattato nella prossima sezione e ci fornirà le
equazioni equivalenti al sistema 1.1, pg. ![]() , equivalenti nel senso che
le soluzioni delle nuove equazioni mi daranno modo di ricavare una
soluzione del sistema 1.1 mediante l'applicazione del Teorema di
equivalenza.
, equivalenti nel senso che
le soluzioni delle nuove equazioni mi daranno modo di ricavare una
soluzione del sistema 1.1 mediante l'applicazione del Teorema di
equivalenza.