Facendo riferimento alla figura 1.6, sia
una curva regolare, C una sottovarietà di dimensione 1 (una curva), la
cui chiusura sia contenuta in un aperto di S e 
un diffeomorfismo
tra l'aperto di 
e la sottovarietà C, poniamo inoltre
e sia , nel caso lorenziano, una curva di tipo
spazio, ovvero 
.
Inoltre se 
indicheremo con 
il modulo di v
definito come
Definizione 1.31 Indichiamo con
il fibrato normale a C e con
la proiezione canonica su C.
Definizione
1.32
Con 
indichiamo, con riferimento alla definizione
1.11
e indichiamo l'applicazione esponenziale `ristretta' a C come
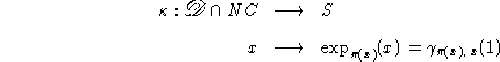
Poichè 
è un aperto contenente 
, esiste
per cui vale:
posto
l'applicazione 
è un rivestimento con 2 fogli su C, quindi poichè C è semplicemente
connesso, 
ha due componenti connesse B' e B''
diffeomorfe attraverso 
a C.
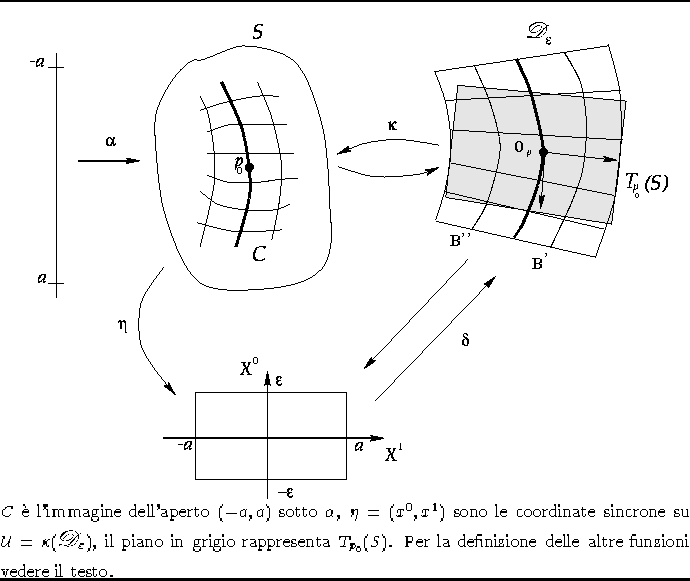
Figura 1.6: Coordinate Sincrone su S.
Fissata una delle due (per esempio B'), l'applicazione
definita ponendo
si avrà che
è un diffeomorfismo con inversa:
L'applicazione 
manda la curva 
in
con vettore tangente in 0 il vettore tangente in 
a C
e la curva 
nella
geodetica 
con vettore tangente in 0
normale in a C.
Da quanto detto e dalla proposizione 1.13 segue che:
è un isomorfismo, e per il teorema dell'applicazione invertibile,
stabilisce un diffeomorfismo tra un intorno di 
e un intorno di
.
Riscegliendo, eventualmente, a e 
possiamo supporre che
sia un diffeomorfismo. Se definisco
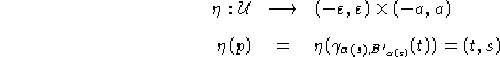
abbiamo che
è un diffeomorfismo, cioè 
è una carta locale ed in questa carta è
evidente che
Indicando le componenti della metrica in questa nuova carta come
osserviamo che vale
Ricordando inoltre che (cfr. [&make_named_href('', "node19.html#onl","[ON]")] pg. 12 e seguenti):
si ha
dunque F è costante lungo le geodetiche, inoltre
Analogamente a quanto abbiamo fatto nella dimostrazione della 1.22, possiamo dire che F è costantemente nulla dato che
e dato che lungo le geodetiche è costante F risulterà nulla su tutto
.
Inoltre dato che non abbiamo fatto altro che un cambio di coordinate, la metrica dovrà essere ancora non singolare ed avere lo stesso indice, quindi deve essere:
