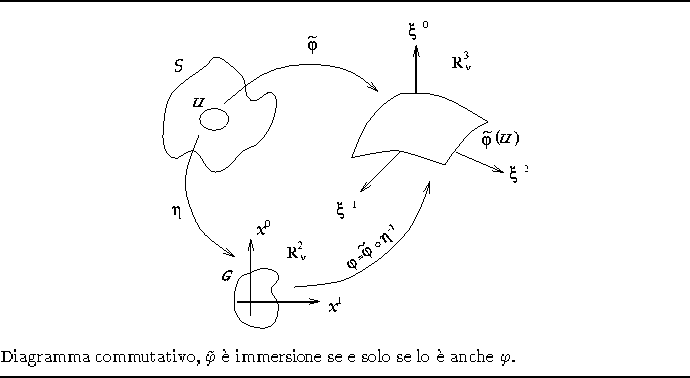
Figura 1.1: Diagramma immersione-carta

Figura 1.1: Diagramma immersione-carta
La notazione introdotta in questa sezione verrà mantenuta per tutto questo capitolo.
Sia S una varietà differenziale bidimensionale (cfr fig.
1.1). ![]() una sua carta, con
una sua carta, con ![]() aperto
di S e
aperto
di S e ![]() di componenti:
di componenti:
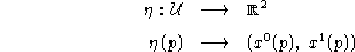
Su ![]() prendiamo un sistema di coordinate
prendiamo un sistema di coordinate ![]() con la metrica canonica definita in forma di matrice come:
con la metrica canonica definita in forma di matrice come:
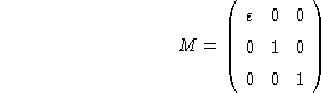
dove ![]() come illustrato nell'introduzione.
Indichiamo il relativo prodotto scalare associato a M con
come illustrato nell'introduzione.
Indichiamo il relativo prodotto scalare associato a M con
![]() definito come:
definito come:
![]()
dove v,w sono due vettori colonna di ![]() .
.
Facendo riferimento alla figura 1.1, consideriamo una generica
immersione ![]() dell'aperto
dell'aperto ![]() di S in
di S in ![]() :
:
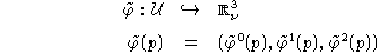
e sia ![]() l'immagine di
l'immagine di ![]() . Sia
. Sia
![]() e
e ![]() .
. ![]() risulterà essere un'immersione dell'aperto
risulterà essere un'immersione dell'aperto ![]() di
di ![]() in
in
![]() . Naturalmente
. Naturalmente ![]() è un'immersione se e solo se lo è anche
è un'immersione se e solo se lo è anche
![]() , dato che
, dato che ![]() è una carta (cfr. [&make_named_href('',
"node19.html#onl","[ON]")]).
Con
è una carta (cfr. [&make_named_href('',
"node19.html#onl","[ON]")]).
Con ![]() indichiamo, il jacobiano di
indichiamo, il jacobiano di ![]() sotto forma di matrice:
sotto forma di matrice:
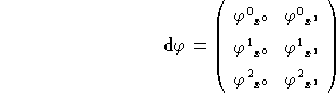
che avrà rango due dato che ![]() è un'immersione e dunque stabilisce
puntualmente un isomorfismo,
è un'immersione e dunque stabilisce
puntualmente un isomorfismo, ![]() ,
,
![]() tra gli spazi vettoriali bidimensionali:
tra gli spazi vettoriali bidimensionali:
![]()
L'isomorfismo cosìprodotto fa sìche la metrica canonica di ![]() induce
canonicamente una metrica su
induce
canonicamente una metrica su ![]() , che grazie alla carta
, che grazie alla carta
![]() è anche una metrica su
è anche una metrica su ![]() , definita puntualmente
come:
, definita puntualmente
come:
![]()
questo esprimendo i vettori di ![]() secondo la base
secondo la base
![]() data dalla carta
data dalla carta ![]() di S.
Che
di S.
Che ![]() sia ben definito come prodotto scalare non degenere
deriva direttamente dalla teoria della geometria differenziale elementare
(cfr. [&make_named_href('',
"node19.html#onl","[ON]")]) e dal fatto che
sia ben definito come prodotto scalare non degenere
deriva direttamente dalla teoria della geometria differenziale elementare
(cfr. [&make_named_href('',
"node19.html#onl","[ON]")]) e dal fatto che ![]() ha rango due essendo una
immersione. Usando per comodità, dato il basso numero di dimensioni,
l'usuale notazione matriciale, si ha:
===
ha rango due essendo una
immersione. Usando per comodità, dato il basso numero di dimensioni,
l'usuale notazione matriciale, si ha:
===
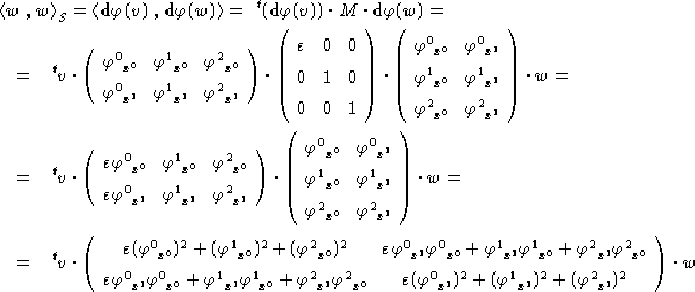
adottando le classiche assegnazioni per le lettere E,F,G:
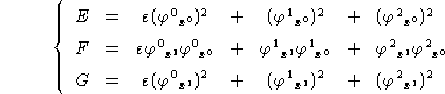
possiamo indicare più comodamente:
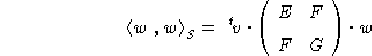
Abbiamo già osservato che ![]() è definito,
differenziabile e di rango due su tutto
è definito,
differenziabile e di rango due su tutto ![]() , quindi anche la metrica
associata alla matrice:
, quindi anche la metrica
associata alla matrice:
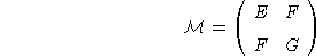
risulterà essere definita, differenziabile e non singolare su tutto
![]() .
.
Riassumendo, in questa sezione abbiamo visto che immergendo l'aperto
della carta di una varietà differenziale bidimensionale in ![]() ,
considerato con la metrica canonica costante M, si induce naturalmente
una metrica
,
considerato con la metrica canonica costante M, si induce naturalmente
una metrica ![]() sull' aperto di partenza. In questo capitolo
vogliamo risolvere il problema inverso:
sull' aperto di partenza. In questo capitolo
vogliamo risolvere il problema inverso:
Assegnata una certa metrica ![]() con matrice
con matrice
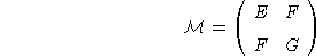
di indice ![]() (
( ![]() o
o ![]() ) su un aperto
) su un aperto ![]() ,
,
![]() carta di una varietà differenziale bidimensionale S,
trovare una immersione isometrica
carta di una varietà differenziale bidimensionale S,
trovare una immersione isometrica ![]() di
di ![]() in
in ![]() ,
detto altrimenti, una immersione tale che la metrica indotta su
,
detto altrimenti, una immersione tale che la metrica indotta su ![]() dalla metrica canonica di
dalla metrica canonica di ![]() sia uguale alla metrica
sia uguale alla metrica ![]() assegnata, ovvero trovare un'immersione
assegnata, ovvero trovare un'immersione ![]() di un
aperto
di un
aperto ![]() di una varietà differenziale bidimensionale S in
di una varietà differenziale bidimensionale S in ![]() e tale che su
e tale che su ![]() sia indotta la metrica
sia indotta la metrica ![]() quando si usano
le coordinate date dalla carta
quando si usano
le coordinate date dalla carta ![]() .
.
Questo equivale a dire, cercare una soluzione su ![]() ,
,
![]() :
:
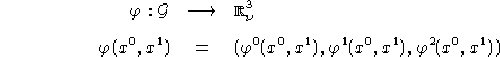
del seguente sistema:
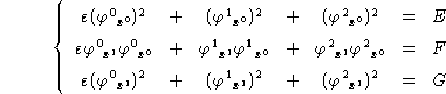
Dato che mediante un cambio di coordinate opportuno (cfr. sez. 1.2) qualunque metrica del tipo
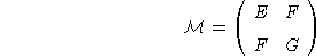
può essere ridotta nella forma diagonale con
![]() , con e=1
, con e=1![]() ,
al posto del precedente sistema cercheremo invece di risolvere il
sistema:
,
al posto del precedente sistema cercheremo invece di risolvere il
sistema:
In generale per un sistema di equazioni non lineare alle derivate parziali del primo ordine del tipo 1.1 non si conoscono soluzioni elementari. Anche la risoluzione semplicemente numerica è problematica data la correlazione non lineare delle derivate parziali. Noi ci accontentiamo di trovare una sola soluzione, anche locale, al sistema 1.1 e non abbiamo restrizioni sulle condizioni iniziali. Anche tenendo conto di queste semplici richieste, non si conoscono soluzioni elementari al sistema 1.1.
Nella sezione 1.3 mostreremo come si può riformulare il problema per ottenere equazioni più facilmente trattabili dal punto di vista numerico e, per casi particolari non banali, come si possono trovare soluzioni simboliche.