1.4 Esplicitazione delle equazioni

 

Considerando R e V nella forma data dalla proposizione 1.35, pg. , considerando i dipendenti in maniera derivabile da , se si sviluppassero i termini della condizione 1.4, pg. del Teorema di Equivalenza:

o più brevemente, sottintendendo la dipendenza attraverso le :

 

si vedrebbe che il sistema risultante, benchè ora sia almeno lineare nelle derivate parziali rispetto le , non è ancora in forma particolarmente comoda.

Cerchiamo un'altra scrittura notando per prima cosa che la proposizione 1.35 ci dice in particolare che R e V nella forma considerata hanno modulo costante. Inoltre in generale se R e V dipendono in maniera differenziale da una generica variabile y, vale sicuramente:

 

Ribadendo che:

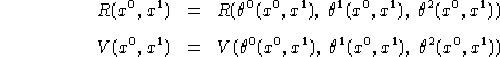
con , come alla proposizione 1.35, riscrivendo l'eq. 1.8 come:

 

e tenendo presente quanto detto possiamo enunciare:

Proposizione  1.37  

Affermo

qualunque sia il valore assunto da e definiti come alla proposizione 1.35, con funzioni arbitrarie derivabili in a valore in .

Dimostrazione Si sfruttano semplicemente le equazioni 1.9, 1.10 e la proposizione 1.35:

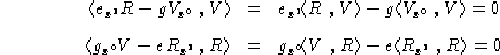
Costruiamo una base alternativa per lo spazio vettoriale che verrà molto utile in seguito.

Lemma  1.38  

Per fissati, la terna di vettori:

con

forma una base ortonormale per lo spazio vettoriale .

Dimostrazione La proposizione 1.35 dimostrata alla fine della precedente sezione ci assicura che i tre vettori della base hanno modulo che non si annulla per qualunque valore degli e ci assicura che:

Per dimostrare che è una base ci manca da mostrare che:

Dimostrato questo, è sicuramente una base dato che è composta da tre vettori non zero e unitari, tra loro perpendicolari a due a due, quindi linearmente indipendenti.

Che è certamente vero, visto come abbiamo definito nella definizione 1.34. Alternativamente si può verificare la relazione direttamente sostituendo nel prodotto scalare le espressioni in coordinate dei due vettori e ricordando le relazioni:

Per ricavare l'equazione 1.10 in coordinate, invece che proiettare i termini usando la base canonica

di possiamo usare la base definita nel precedente lemma essendo quest'ultima ortonormale, ottenendo:

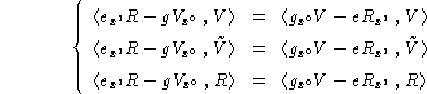
Sviluppando i prodotti, tenendo conto dell'equazione 1.9, pg. , delle proposizioni 1.37, pg. , 1.35, pg. e del lemma 1.38, pg. , otteniamo:

 

allora le equazioni 1.11 diventano nel caso lorenziano, sviluppando pedestremente i prodotti scalari:

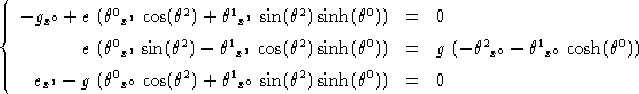
Caso riemanniano:

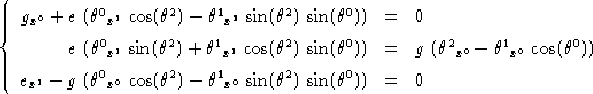
Questi 2 sistemi saranno la versione in coordinate nei due casi dell'equazione vettoriale 1.8. Se teniamo conto che e=1 otteniamo:

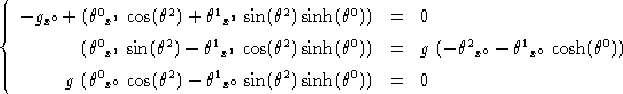
Caso riemanniano:

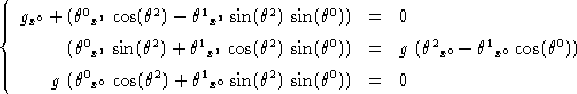
Per riassumere quanto detto finora raccogliamo i risultati ottenuti dalla discussione nel seguente teorema:

Teorema  1.39 [dell'Immersione]  

Siano e,g funzioni a valori in di derivabili, definite e mai nulle su . Se le funzioni :

sono soluzioni, nel caso lorenziano, del sistema:

 

e nel caso riemanniano soluzioni di: ===

 

=== Allora se R e V sono due vettori definiti nel caso lorenziano come:

e nel caso riemanniano come: ===

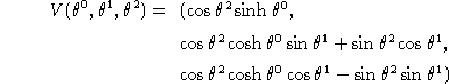
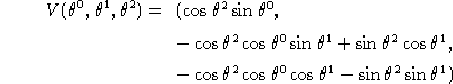
=== dipendenti da mediante le soluzioni di 1.12 (1.13):

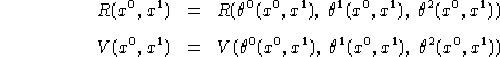
la funzione definita su come:

con , e fissati a piacere, parametrizza una superfice in che risulta avere come metrica indotta, espressa in forma di matrice:

ovvero soddisfa il sistema 1.1, pg. ed è un'immersione dell'aperto di in .

Dimostrazione Se le sono funzioni di soluzioni dell'eq. 1.12 (eq.1.13) soddisferanno anche le eq. 1.10, pg. e quindi l'eq. 1.8, pg. sarà soddisfata e dunque è verificata la condizione 1.4, pg. . Inoltre R e V per la proposizione 1.35, pg. soddisfano l'equazioni 1.3, pg. e quindi si può applicare il Teorema di Equivalenza per calcolare esplicitamente l'immersione isometrica voluta.

In generale per trovare l'immersione data una certa metrica basta che troviamo, dati e e g, una soluzione

del sistema 1.12 (1.13), sostituendola in e in ottenendo

e applicando il Th. di Immersione trovo che è l'immersione cercata.

Quindi l'unico vero problema che rimane per calcolare è trovare le soluzioni al sistema 1.12 (eq.1.13). Nel prossimo capitolo vedremo come si possono ottenere delle soluzioni simboliche quando aggiungiamo delle restrizioni alla forma della metrica, restrizioni che tuttavia mostreremo racchiudere comunque un'ampia famiglia di superfici.