2.3 Immersione metriche generiche.

 

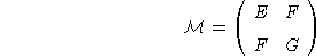
Nel caso generale avremo una generica matrice non degenere

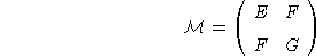
a cui applicando uno dei metodi illustrati nella sezione 1.2 otteremo una matrice diagonale nella forma:

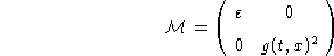
E quindi possiamo applicare il Teorema di Immersione (cfr. 1.39, pg. ) da cui otteniamo il sistema da risolvere, che nel caso lorenziano è:

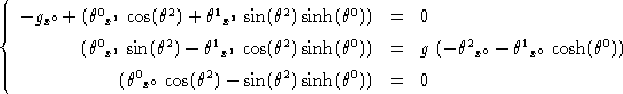
e nel caso riemanniano:

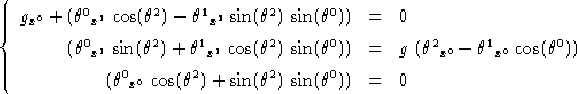
Osserviamo subito che dalle prime due equazioni di ogni sistema possiamo esplicitare le derivate . Posto, per abbreviare la scrittura delle equazioni, le seguenti uguaglianze:

===

=== Ricaviamo , dai sistemi precedenti ottenendo:

 

Caso riemanniano:

 

Questo è un sistema di equazioni differenziali del primo ordine alle derivate parziali quasi lineare. Notare che dalla terza equazione del sistema 2.22 (2.23) possiamo ricavare per ogni (t,x) del dominio di definizione di g(t,x) con , dove

===

=== allora

 

===

 

=== e se è soluzione lo è anche .

In generale trovare una soluzione esplicita ai sistemi 2.23, 2.22 non è detto sia possibile, dovremo quindi accontentarci di un algoritmo numerico.

Basandoci su un algoritmo numerico per sistemi di equazioni differenziali del primo ordine alle derivate parziali quasi lineare a coefficenti costanti (cfr. [&make_named_href('', "node19.html#vll","[VLL]")]) abbiamo sviluppato il seguente algoritmo per risolvere il sistema 2.22 (2.23):

 
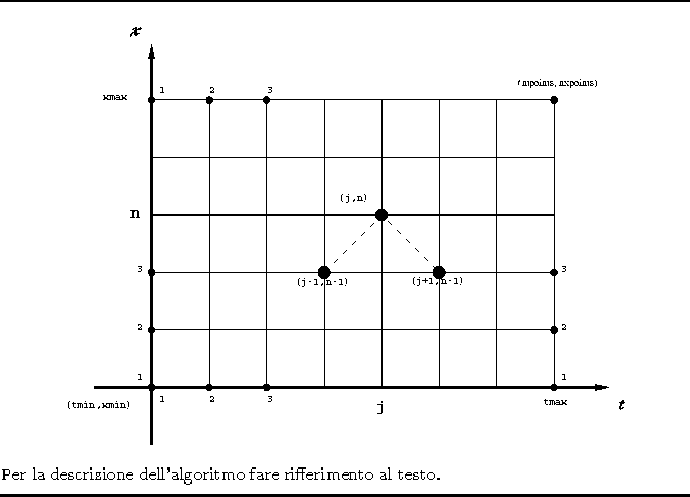
Figura 2.10: Griglia base algoritmo caso generale. 

Ingresso:

ep,g:

, .

xmin,xmax:

Intervallo in cui varia x.

tmin,tmax:

Intervallo in cui varia t.

ntpoints,nxpoints:

Numero dei punti in cui suddividere rispettivamente l'intervallo e . Con j, si indica l'indice dei punti lungo t. Con, n si indica l'indice dei punti lungo x. Cfr. figura 2.10.

Passi:

1. Prelievo dei dati in ingresso.
2. Calcolo le condizioni iniziali restringendo g alla retta usando le 2.5 (2.9) con e per il caso riemanniano mentre nel caso lorenziano prendiamo .
3. calcolo la distanza tra i punti lungo t e lungo x con

   

   

4. Pongo n=2
5. Calcolo numericamente le derivate e a . Dato come abbiamo calcolato le condizioni iniziali, avremo =0
6. Se FINE.
7. Calcolo con ricavandolo da:

   

8. e lo calcolo estrapolandolo da una spline passante per i punti e
9. Calcolo con ricavandolo da:

   

10. e lo calcolo estrapolandolo da una spline passante per i punti e
11. Dalla terza equazione del sistema applicando le 2.24 (2.25) ottengo l'angolo . Per j>2, scelgo il segno di che mi rende più piccola la differenza .
12. Calcolo nuovamente numericamente le derivate di lungo t,
13. Controllo che non sia prossimo a 0 altrimenti avverto della presenza di un possibile punto critico ad
14. incremento n di 1 e vado al passo (v)

Una volta ottenuta una approssimazione di sui punti non mi resta che applicare il Teorema dell'Immersione per ottenere la superfice cercata.

L'algoritmo utilizzato per calcolare le derivate è principalemente quello riportato su [&make_named_href('', "node19.html#cas","[CAS]")] pg. 92. Per l'intergrazione si è usato l'algoritmo impiegato dalla funzione di libreria di Mathematica Calculus`ListIntegrate` modificato per restituire un'approssimazione della funzione integrale.