2.2 Esempi di immersione per metriche decomponibili.

 

In quest sezione mostiramo come si applica il Teorema di Immersione per metriche decomponibili ad alcune metriche comuni.

 
Figura 2.3: Elica. 

Esempio  2.6  

Prendiamo la metrica:

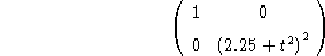
ovvero mantenendo la notazione corrente:

con condizioni iniziali:

Con questi dati possiamo calcolare che sarà pari a: Applicando le formule del teorema 2.5 per il caso riemanniano viene

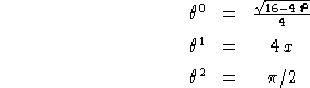
Sostituendo questi valori nelle formule per date sempre dal teorema dell'immersione otteniamo, prendendo :

 

La superfice cosìottenuta possiamo osservarla nella figura 2.3 disegnata nell'intervallo .

 
Figura 2.4: Iperboloide. 

Esempio  2.7  

Prendiamo la metrica:

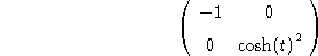
ovvero mantenendo la notazione corrente:

con condizioni iniziali:

Con questi dati possiamo calcolare che sarà pari a: Applicando le formule del teorema 2.5 per il caso lorenziano viene

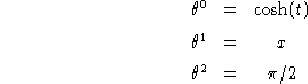
Sostituendo questi valori nelle formule per date sempre dal teorema dell'immersione otteniamo, prendendo :

 

La superfice cosìottenuta possiamo osservarla nella figura 2.4 disegnata nell'intervallo .

 
Figura 2.5: Ipersfera. 

Esempio  2.8  

Prendiamo la metrica:

ovvero mantenendo la notazione corrente:

con condizioni iniziali:

Con questi dati possiamo calcolare che sarà pari a: Applicando le formule del teorema 2.5 per il caso riemanniano viene

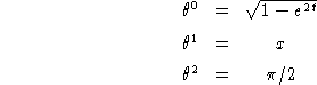
Sostituendo questi valori nelle formule per date sempre dal teorema dell'immersione otteniamo, prendendo :

 

La superfice cosìottenuta possiamo osservarla nella figura 2.5 disegnata nell'intervallo .

 
Figura 2.6: Sfera. 

Esempio  2.9  

Prendiamo la metrica:

ovvero mantenendo la notazione corrente:

con condizioni iniziali:

Con questi dati possiamo calcolare che sarà pari a: Applicando le formule del teorema 2.5 per il caso riemanniano viene

Sostituendo questi valori nelle formule per date sempre dal teorema dell'immersione otteniamo, prendendo :

 

La superfice cosìottenuta possiamo osservarla nella figura 2.6 disegnata nell'intervallo .

 
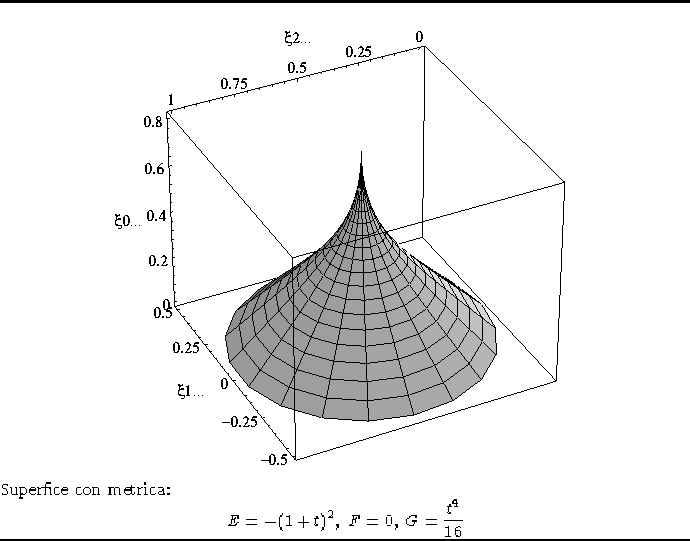
Figura 2.7: Metrica generica 1. 

Esempio  2.10  

Prendiamo la metrica:

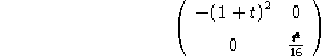
ovvero mantenendo la notazione corrente:

con condizioni iniziali:

Con questi dati possiamo calcolare che sarà pari a: Applicando le formule del teorema 2.5 per il caso lorenziano viene

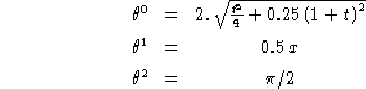
Sostituendo questi valori nelle formule per date sempre dal teorema dell'immersione otteniamo, prendendo :

 

La superfice cosìottenuta possiamo osservarla nella figura 2.7 disegnata nell'intervallo .

 
Figura 2.8: Toro. 

Esempio  2.11  

Prendiamo la metrica:

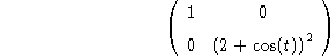
ovvero mantenendo la notazione corrente:

con condizioni iniziali:

Con questi dati possiamo calcolare che sarà pari a: Applicando le formule del teorema 2.5 per il caso riemanniano viene

Sostituendo questi valori nelle formule per date sempre dal teorema dell'immersione otteniamo, prendendo :

 

La superfice cosìottenuta possiamo osservarla nella figura 2.8 disegnata nell'intervallo .

 
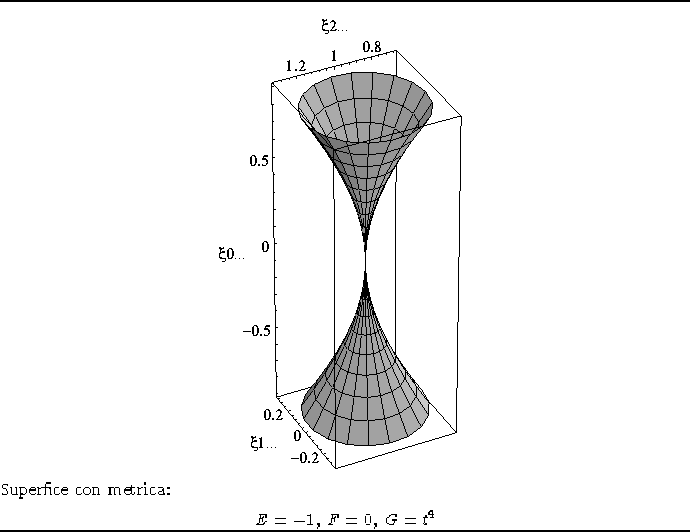
Figura 2.9: Metrica generica 2. 

Esempio  2.12  

Prendiamo la metrica:

ovvero mantenendo la notazione corrente:

con condizioni iniziali:

Con questi dati possiamo calcolare che sarà pari a: Applicando le formule del teorema 2.5 per il caso lorenziano viene

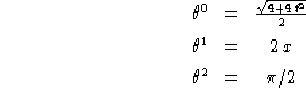
Sostituendo questi valori nelle formule per date sempre dal teorema dell'immersione otteniamo, prendendo :

 

La superfice cosìottenuta possiamo osservarla nella figura 2.9 disegnata nell'intervallo .