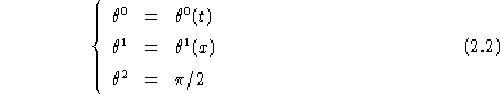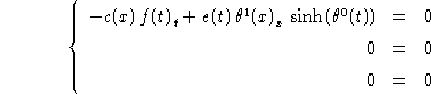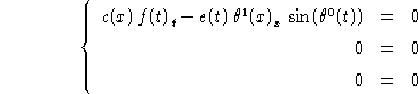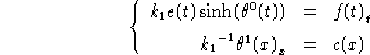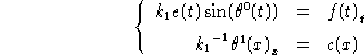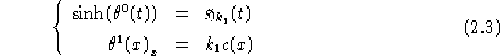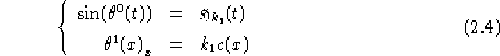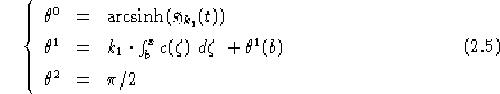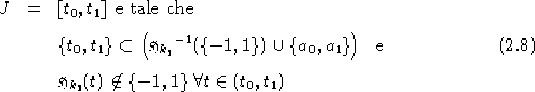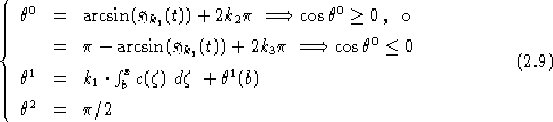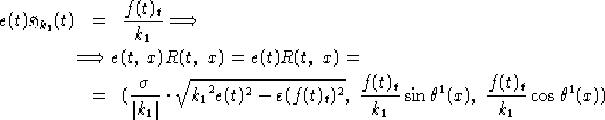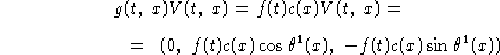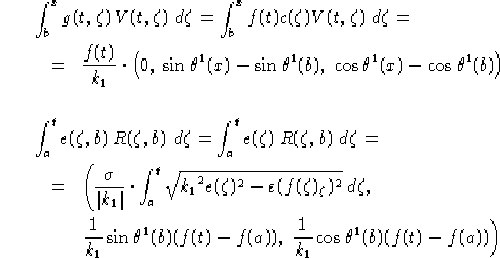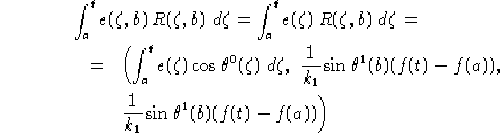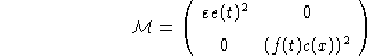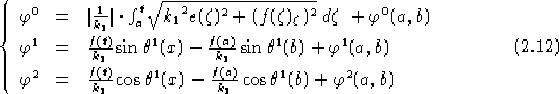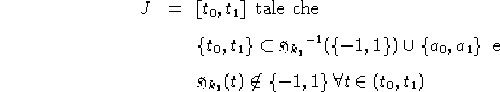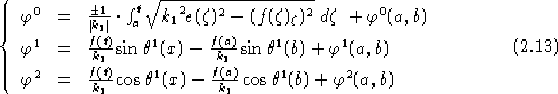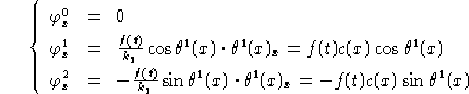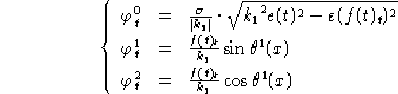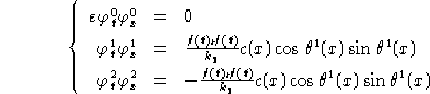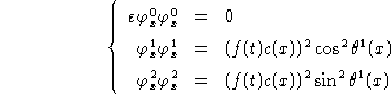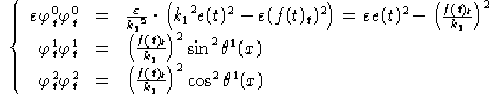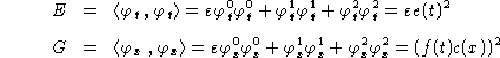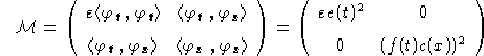


Next: 2.2 Esempi di immersione
Up: 2 Calcolo Immersioni.
Previous: 2 Calcolo Immersioni.
Definizione
2.1
Sia  una metrica definita su un aperto
una metrica definita su un aperto
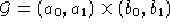 di
di 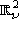 con coordinate
indicate con (t,x) e le componenti
con coordinate
indicate con (t,x) e le componenti
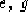 della metrica abbiano una dipendenza da (t,x) del tipo:
della metrica abbiano una dipendenza da (t,x) del tipo:
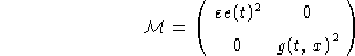
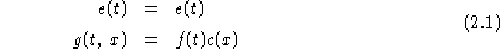
con e(t), f(t) funzioni continue strettamente positive dipendenti
esclusivamente da t, f(t) derivabile ed entrambe definite
sull'intervallo reale 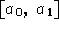 , c(x) funzione continua
strettamente positiva dipendente esclusivamente da x e definita
sull'intervallo reale
, c(x) funzione continua
strettamente positiva dipendente esclusivamente da x e definita
sull'intervallo reale 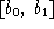 .
. 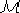 la chiamiamo
Metrica decomponibile.
la chiamiamo
Metrica decomponibile.
Se siamo nel contesto della definizione 2.1, è possibile
trovare delle soluzioni esplicite alle 1.12, pg. 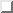 (1.13, pg.
(1.13, pg.  )
ipotizzando che le soluzioni in
)
ipotizzando che le soluzioni in 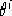 abbiano la forma:
abbiano la forma:
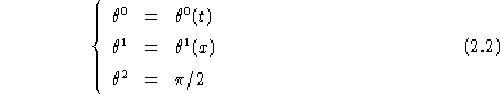
con 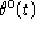 e
e 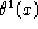 funzioni incognite e
funzioni incognite e 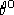 dipendente solo e
soltanto dalla variabile t e
dipendente solo e
soltanto dalla variabile t e 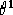 dipendente solo e soltanto dalla
variabile x.
dipendente solo e soltanto dalla
variabile x.
Facendo queste ipotesi e sostituendo nel sistema 1.12
(1.13) si ottiene:
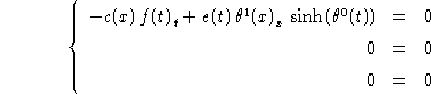
===
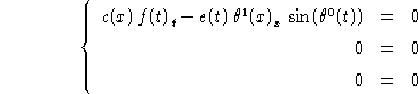
===
da cui, sapendo che 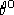 dipende solo da t e che
dipende solo da t e che 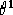 dipende solo
da x, siamo obbligati ad avere:
dipende solo
da x, siamo obbligati ad avere:
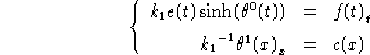
===
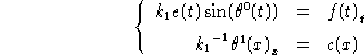
===
Con 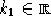 una costante non nulla. Definendo per comodità:
una costante non nulla. Definendo per comodità:
Definizione
2.2
In entrambi i casi, lorenziano e riemanniano, poniamo:

che risulterà una funzione definita su tutto 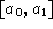 , continua, e
, continua, e
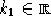 costante non nulla.
costante non nulla.
Facendo uso di questa definizione potremo scrivere più brevemente:
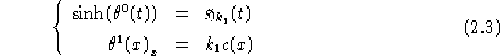
===
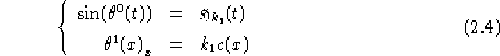
===
Nel caso lorenziano è facile trovare una soluzione, infatti è facile vedere
che soluzioni per 2.3 sono:
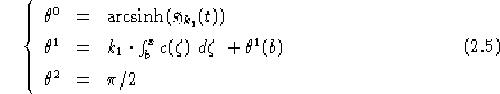
con 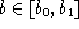 fissato,
fissato, 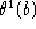 valore iniziale scelto a piacere.
Nel caso riemanniano (equazione 2.4) possiamo ricavare
tranquillamente
valore iniziale scelto a piacere.
Nel caso riemanniano (equazione 2.4) possiamo ricavare
tranquillamente 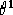 essendo l'equazione relativa uguale a quella del caso
lorenziano, ottenenedo:
essendo l'equazione relativa uguale a quella del caso
lorenziano, ottenenedo:
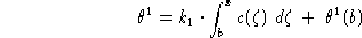
Per quanto riguarda la determinazione dell'angolo 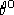 sorgono
spontaneamente due problemi:
sorgono
spontaneamente due problemi:
Problema
2.3
La funzione 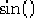 varia tra [-1,1] e quindi la prima equazione delle
2.4
varia tra [-1,1] e quindi la prima equazione delle
2.4

avrà soluzione solo per valori di 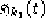 compresi in
[-1,1]
compresi in
[-1,1]
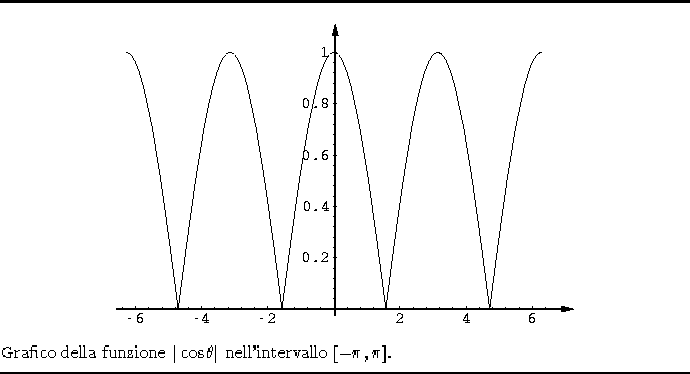
Figura 2.2: Funzione 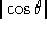 .
.
Problema
2.4
La funzione 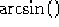 è definita come funzione inversa della funzione
è definita come funzione inversa della funzione
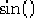 solo tra gli intervalli:
solo tra gli intervalli:
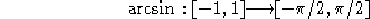
e si ha, sempre per definizione di 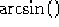 :
:

e 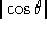 in generale non è derivabile nei punti in cui
in generale non è derivabile nei punti in cui
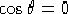 (cfr fig. 2.1) o, equivalentemente,
(cfr fig. 2.1) o, equivalentemente,
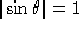 .
.
Quando vogliamo calcolare 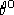 nel caso riemanniano dalle equazioni
2.3 otteniamo efettivamente solo il valore di
nel caso riemanniano dalle equazioni
2.3 otteniamo efettivamente solo il valore di 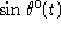 e,
come vedremo, ci serve conoscere una determinazione differenziabile di
e,
come vedremo, ci serve conoscere una determinazione differenziabile di
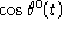 , ma a causa di quanto esposto, se lo calcoliamo mediante
l'uso della funzione
, ma a causa di quanto esposto, se lo calcoliamo mediante
l'uso della funzione 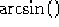 , otteniamo una funzione
, otteniamo una funzione 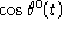 che
potenzialmente è non derivabile nell'insieme, possibilmente vuoto:
che
potenzialmente è non derivabile nell'insieme, possibilmente vuoto:
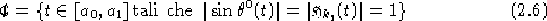
ed in questi punti il sistema 1.13 potrebbe non essere definito,
e l'insieme 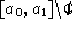 viene suddiviso in tante
componenti conesse quanti sono gli elementi di
viene suddiviso in tante
componenti conesse quanti sono gli elementi di 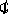 più uno e su
ognuna sono definite soluzioni potenzialmente differenti. La situazione
ideale che voremo avere è quella di conoscere un'unica soluzione
definita su tutto
più uno e su
ognuna sono definite soluzioni potenzialmente differenti. La situazione
ideale che voremo avere è quella di conoscere un'unica soluzione
definita su tutto 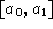 in modo che
in modo che 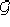 una volta immerso in
una volta immerso in
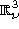 risulti essere un'unica superfice conessa.
risulti essere un'unica superfice conessa.
Soluzione problema 2.3
Il problema causato dalla limitazione della funzione
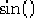 è facilmente agirabile, infatti essendo
è facilmente agirabile, infatti essendo 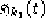 , per valori
di
, per valori
di 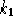 non nulli, una funzione continua sul compatto
non nulli, una funzione continua sul compatto 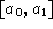 , segue
che possiede minimo e massimo, e quindi, se
, segue
che possiede minimo e massimo, e quindi, se 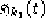 non è costantemente
nulla
non è costantemente
nulla ,
scegliendo
,
scegliendo 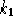 in modo che soddisfi:
in modo che soddisfi:
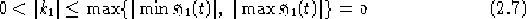
si ha evidentemente che per questi valori di  la funzione
la funzione  assumerà valori solo nell'intervallo [-1,1].
assumerà valori solo nell'intervallo [-1,1].

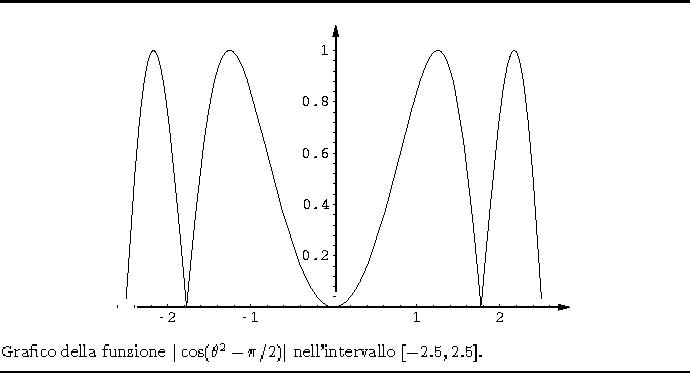
Figura: Funzione 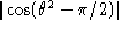 .
.
Soluzione problema 2.4
Per risolvere questo problema, o troviamo con metodi euristici una
funzione 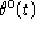 che soddisfa la prima equazione delle 2.4
(cfr. esempio 2.9) e definita su tutto
che soddisfa la prima equazione delle 2.4
(cfr. esempio 2.9) e definita su tutto 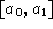 o ci
accontentiamo nel caso riemanniano di una soluzione locale definita in
intervalli del tipo
o ci
accontentiamo nel caso riemanniano di una soluzione locale definita in
intervalli del tipo
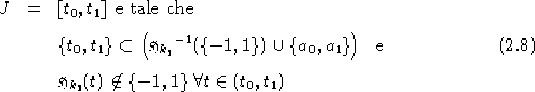
che sono tali che, con 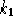 soddisfacente la condizione data dalla
2.7,
soddisfacente la condizione data dalla
2.7, 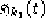 calcolata su un intervallo J
soddisfacente la condizione 2.8, assume valore 1 o -1
al più agli estremi dell'intervallo. Notare che se
calcolata su un intervallo J
soddisfacente la condizione 2.8, assume valore 1 o -1
al più agli estremi dell'intervallo. Notare che se 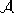 è una
componente conessa di
è una
componente conessa di 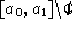 , la chiusura
, la chiusura
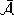 soddisfa la condizione data da 2.8.
soddisfa la condizione data da 2.8.
Volendo, come soluzione alternativa, si potrebbe anche scegliere

avendo così 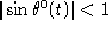 per
per 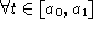 e quindi non si
passerebbe mai per i punti di possibile non derivabilità di
e quindi non si
passerebbe mai per i punti di possibile non derivabilità di
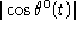 corrispondenti ai punti dove
corrispondenti ai punti dove 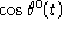 cambia di segno,
e quindi
cambia di segno,
e quindi 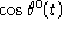 avrebbe segno costante per ogni
avrebbe segno costante per ogni 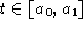 .
Parliamo di punti di possibile non derivabilità perchè se consideriamo ad
esempio la funzione
.
Parliamo di punti di possibile non derivabilità perchè se consideriamo ad
esempio la funzione 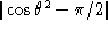 , nel punto
, nel punto 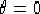 la
funzione è nulla ma è derivabile in tale punto, infatti
la
funzione è nulla ma è derivabile in tale punto, infatti
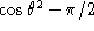 nell'intorno di
nell'intorno di 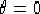 non cambia di segno,
cfr. figura 2.2
non cambia di segno,
cfr. figura 2.2
Teoricamente per via numerica si può anche risolvere il problema
2.4 se si conosce l'insieme 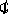 , infatti basta far
cambiare segno alla funzione ogni volta che si attraversa un punto
, infatti basta far
cambiare segno alla funzione ogni volta che si attraversa un punto
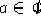 e
e 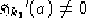 perchè se fosse zero
componendola con la funzione valore assoluto non si introducono
discontinuità nella derivata prima perchè la derivata destra e sinistra
di
perchè se fosse zero
componendola con la funzione valore assoluto non si introducono
discontinuità nella derivata prima perchè la derivata destra e sinistra
di 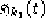 in a sarebbe zero e quindi derivabile in un intorno di a
in a sarebbe zero e quindi derivabile in un intorno di a

Concludendo, riguardo alle soluzione di 2.4 per il caso riemanniano,
possiamo dire, eventualmente restringendo l'intervallo 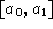 in cui
varia la variabile t ad un intervallo che soddisfa le condizioni della
2.8, (cfr. discussione problema 2.4):
===
in cui
varia la variabile t ad un intervallo che soddisfa le condizioni della
2.8, (cfr. discussione problema 2.4):
===
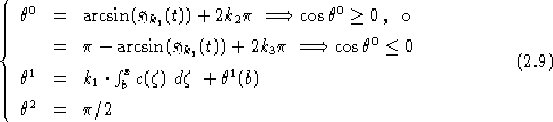
===
Con 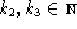 costanti arbitrarie.
costanti arbitrarie.
Ora che abbiamo delle soluzioni al sistema 1.12, pg.  (1.13, pg.
(1.13, pg.  ) possiamo applicare il Teorema dell'immersione.
Calcoliamo l'espressione di
) possiamo applicare il Teorema dell'immersione.
Calcoliamo l'espressione di 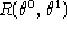 e
e 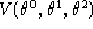 tenendo conto che le
equazioni 2.3 (2.4) ci danno direttamente il valore
di
tenendo conto che le
equazioni 2.3 (2.4) ci danno direttamente il valore
di 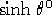 (
( 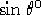 ) e che
) e che
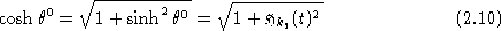
===
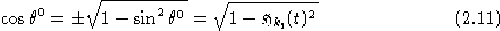
===
Ottenendo, tenendo presente le note fatte per il problema 2.4
riguardo il dominio di definizione e di derivabilità per il caso riemanniano
di 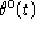 e
e 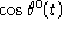 :
:
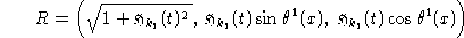
===
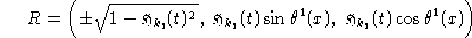
===
o più brevemente, ponendo 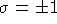 nel caso riemanniano e
nel caso riemanniano e 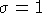 nel
caso lorenziano:
nel
caso lorenziano:
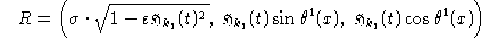
Per quanto rigurda V in entrambi i casi si ha:
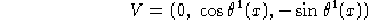
Dal teorema di immersione abbiamo che l'immersione 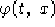 è data da
è data da
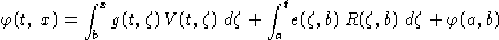
con 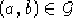 fissato e
fissato e 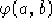 condizione iniziale. Tenendo
conto della definizione 2.2 di
condizione iniziale. Tenendo
conto della definizione 2.2 di 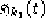 e che e(t)>0
abbiamo:
e che e(t)>0
abbiamo:
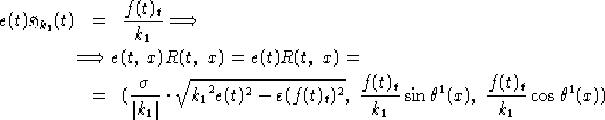
Nel caso riemanniano può essere più comodo avere la componente 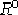 espressa come
espressa come
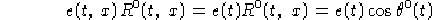
Per quanto riguarda la componente di 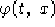 ottenuta da V:
ottenuta da V:
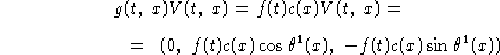
da cui, ricordando che dalle 2.9 si ha 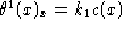 ,
i due integrali che danno
,
i due integrali che danno  saranno:
saranno:
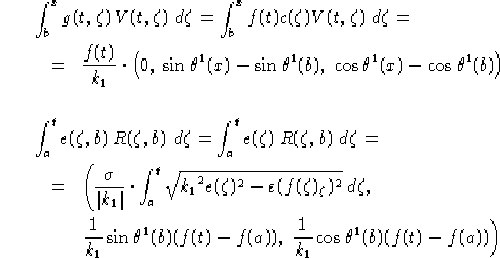
Con  ,
, 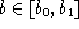 condizione iniziale scelta a piacere.
Inoltre se si conosce
condizione iniziale scelta a piacere.
Inoltre se si conosce 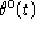 definita su tutto
definita su tutto 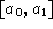 e soluzione di
2.4, possiamo scrivere:
e soluzione di
2.4, possiamo scrivere:
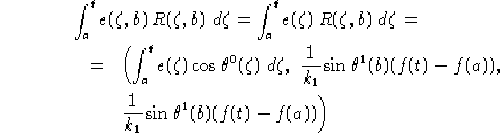
Sostituendo i risultati intermedi nell'espressione di 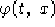 otteniamo,
con
otteniamo,
con 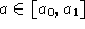 fissato:
fissato:

Nel caso lorenziano puo fare più comodo esprimere la componente 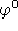 come
come
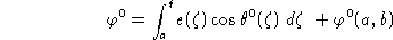
Riassumiamo quanto detto in questa sezione in un unico teorema:
Teorema
2.5
[Immersione per metriche decomponibili]
Sia 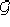 un aperto di
un aperto di 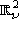 del tipo
del tipo
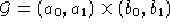 ,
, 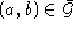 un punto
fissato.
Sia
un punto
fissato.
Sia 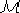 una metrica decomponibile definita su
una metrica decomponibile definita su
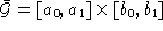 e le coordinate siano indicate simbolicamente con
e le coordinate siano indicate simbolicamente con 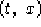 .
.
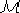 espresso in forma matriciale sia:
espresso in forma matriciale sia:
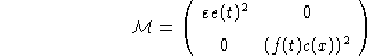
Ponendo

con 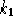 costante reale non nulla con la richiesta che nel caso
riemanniano soddisfi la condizione:
costante reale non nulla con la richiesta che nel caso
riemanniano soddisfi la condizione:
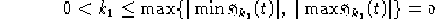
Allora, ponendo 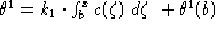 ,
nel caso lorenziano la funzione
,
nel caso lorenziano la funzione 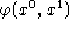 definita per componenti come:
definita per componenti come:
è un'immersione isometrica locale di 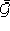 in
in 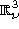 .
.
Inoltre nel caso riemanniano se 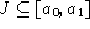 è un intorno soddisfacente
è un intorno soddisfacente
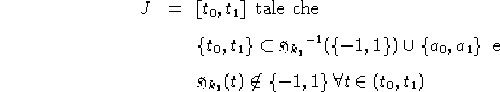
Si ha, ponendo
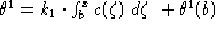 , che la funzione
===
, che la funzione
===
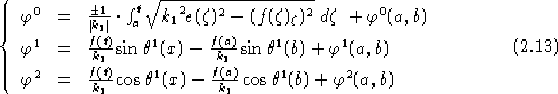
===
è un'immersione locale di 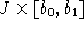 in
in 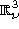 . Se inoltre
si conosce una funzione
. Se inoltre
si conosce una funzione 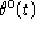 definita e derivabile su tutto
definita e derivabile su tutto
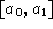 con
con

allora la componente 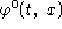 diventa:
diventa:
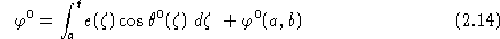
e  cosìdefinita è un'immersione isometrica locale per
cosìdefinita è un'immersione isometrica locale per
 in
in 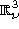 .
.
Dimostrazione
Ovvia da quanto detto in questa sezione, comunque per verifica mostriamo
che la metrica indotta da 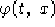 è propio la metrica cercata.
Deriviamo
è propio la metrica cercata.
Deriviamo 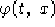 per x e t tenendo conto che
per x e t tenendo conto che 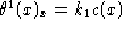 :
:
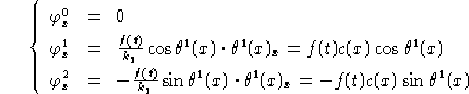
per le derivate lungo t, prendendo 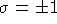 nel caso riemanniano e
nel caso riemanniano e
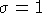 nel caso lorenziano, abbiamo:
nel caso lorenziano, abbiamo:
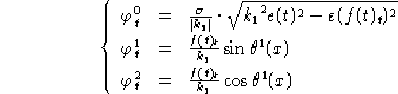
e nel caso riemanniano, usando la forma di 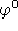 data dall'equazione
2.14:
data dall'equazione
2.14:

Calcoliamo le componenti di 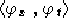
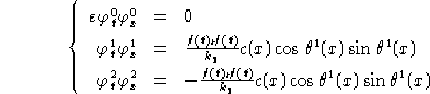
e dunque:
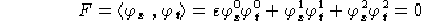
Ed ora le componenti di 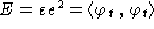 ed
ed
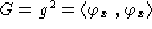 :
:
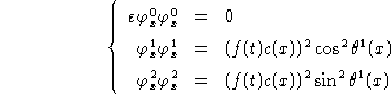
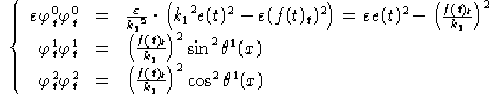
e dunque:
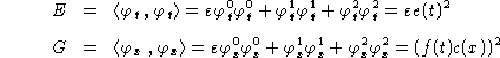
e quindi la metrica indotta dalla metrica canonica di 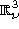 sulla
superfice parametrizzata da
sulla
superfice parametrizzata da 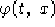 risulta essere:
risulta essere:
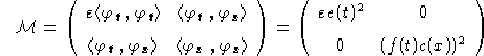




Next: 2.2 Esempi di immersione
Up: 2 Calcolo Immersioni.
Previous: 2 Calcolo Immersioni.
Charlie &
Tue Sep 24 00:18:57 PDT 1996
![]() una metrica definita su un aperto
una metrica definita su un aperto
![]() di
di ![]() con coordinate
indicate con (t,x) e le componenti
con coordinate
indicate con (t,x) e le componenti
![]() della metrica abbiano una dipendenza da (t,x) del tipo:
della metrica abbiano una dipendenza da (t,x) del tipo:
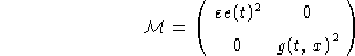
![]()
![]() , c(x) funzione continua
strettamente positiva dipendente esclusivamente da x e definita
sull'intervallo reale
, c(x) funzione continua
strettamente positiva dipendente esclusivamente da x e definita
sull'intervallo reale ![]() .
. ![]() la chiamiamo
Metrica decomponibile.
la chiamiamo
Metrica decomponibile.