
Definizione 1.1 Una geodetica di una varietà differenziale S è una curva

il cui campo vettoriale ![]() è paralello, detto altrimenti
l'accelerazione
è paralello, detto altrimenti
l'accelerazione ![]() della curva è nulla.
della curva è nulla.
Corollario
1.2
Sia ![]() con
con ![]() una carta per S. Una curva
una carta per S. Una curva ![]() in
in
![]() è una geodetica di S se e solo se le sue coordinate
è una geodetica di S se e solo se le sue coordinate
![]()
soddisfano
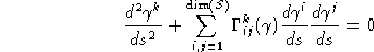
.
Dimostrazione Cfr. [&make_named_href('', "node19.html#onl","[ON]")].
Il teorema di esistenza e unicità delle equazioni differenziali ordinarie ci dà il seguente risultato:
Lemma
1.3
Se ![]() esiste un intervallo I di 0 ed un'unica geodetica
esiste un intervallo I di 0 ed un'unica geodetica
![]()
tale che ![]() e
e ![]() .
.
Dimostrazione Cfr. [&make_named_href('', "node19.html#onl","[ON]")].
Lemma
1.4
Siano ![]() geodetiche. Se esiste un numero
geodetiche. Se esiste un numero
![]() tale che
tale che ![]() , allora
, allora ![]() .
.
Dimostrazione Cfr. [&make_named_href('', "node19.html#onl","[ON]")].
Proposizione
1.5
Dato un vettore tangente ![]() esiste un'unica geodetica
esiste un'unica geodetica
![]()
tale che:
Dimostrazione Cfr. [&make_named_href('', "node19.html#onl","[ON]")].
D'ora in poi quando parleremo di geodetiche intenderemo sempre parlare di geodetiche massimali, se non specificato altrimenti.
Definizione
1.6
Una varietà differenziale S si dice geodeticamente completa o
semplicemente completa se ogni geodetica massimale è definita su
tutto ![]() .
.
Esempio
1.7
[Geodetiche in
ottenendo ![]() ]
Consideriamo
]
Consideriamo ![]() con la metrica cannonica lorenziana o euclidea. In
questo caso i simboli di Christoffel sono nulli e dunque l'equazione che
dà le geodetiche si riduce a:
con la metrica cannonica lorenziana o euclidea. In
questo caso i simboli di Christoffel sono nulli e dunque l'equazione che
dà le geodetiche si riduce a:
![]()
![]() con
con ![]() e
e ![]() costanti arbitrarie.
Immediata conseguenza è che le geodetiche non costanti di
costanti arbitrarie.
Immediata conseguenza è che le geodetiche non costanti di ![]() ,
considerato con la relativa metrica canonica, sono le rette.
,
considerato con la relativa metrica canonica, sono le rette.
Lemma
1.8
Sia ![]() una geodetica non costante. Una
riparametrizzazione
una geodetica non costante. Una
riparametrizzazione ![]() è ancora una geodetica se e
solo se h(t)=at+b.
è ancora una geodetica se e
solo se h(t)=at+b.
Dimostrazione Cfr. [&make_named_href('', "node19.html#onl","[ON]")].
Lemma
1.9
Sia v un vettore tangente ad S, ![]() . Allora esiste un intorno
. Allora esiste un intorno
![]() di
di ![]() in TS e un intervallo I intorno a 0 tale che la
mappa definita da:
in TS e un intervallo I intorno a 0 tale che la
mappa definita da:

è ben definita e differenziabile.
Dimostrazione Cfr. [&make_named_href('', "node19.html#onl","[ON]")].
Proposizione
1.10
Esiste un campo vettoriale G in TS tale che se ![]() è la
proiezione canonica vale:
è la
proiezione canonica vale:
![]()
ovvero detto altrimenti esiste una biiezione tra le curve integrali (massimali) di G e le geodetiche (massimali) di S.
Dimostrazione Cfr. [&make_named_href('', "node19.html#onl","[ON]")].
Definizione
1.11
Se
tale che ![]() , sia
, sia ![]() l'insieme dei vettori v in
l'insieme dei vettori v in
![]() tali che la geodetica inestensibile
tali che la geodetica inestensibile ![]() è definita
almeno nell'intervallo reale [0,1]. La mappa esponenziale di S
in o è la funzione
è definita
almeno nell'intervallo reale [0,1]. La mappa esponenziale di S
in o è la funzione
![]()
![]() .
.
Naturalmente ![]() è il più grande sottinsieme di
è il più grande sottinsieme di ![]() sul quale
sul quale ![]() può essere definita, ed è immediato che se S è
completo nel senso della def. 1.6, allora
può essere definita, ed è immediato che se S è
completo nel senso della def. 1.6, allora
![]() .
.
Osservazione 1.12 Osservando l'equazione delle geodetiche (cfr definizione 1.1) si vede che deve valere:
![]()
e quindi si ha una corrispondenza tra le rette attraverso l'origine di
![]() e le geodetiche di S passanti per o.
e le geodetiche di S passanti per o.
Proposizione
1.13
Per ogni punto o di S esiste un intorno ![]() di
0 in
di
0 in ![]() per il quale la mappa esponente
per il quale la mappa esponente ![]() è un
diffeomorfismo con
è un
diffeomorfismo con ![]() intorno di o in S.
intorno di o in S.
Dimostrazione Cfr. [&make_named_href('', "node19.html#onl","[ON]")] pg. 70.
Definizione
1.14
Con riferimento alla proposizione precedente, se ![]() è
anche stellato, allora
è
anche stellato, allora ![]() è detto intorno normale di
o.
è detto intorno normale di
o.
Proposizione
1.15
Se ![]() è un intorno normale di
è un intorno normale di ![]() , allora
, allora
![]() esiste un'unica geodetica
esiste un'unica geodetica
![]()
da o in p tutta contenuta in ![]() . Inoltre vale
. Inoltre vale
![]() .
.
Dimostrazione Cfr. [&make_named_href('', "node19.html#onl","[ON]")].
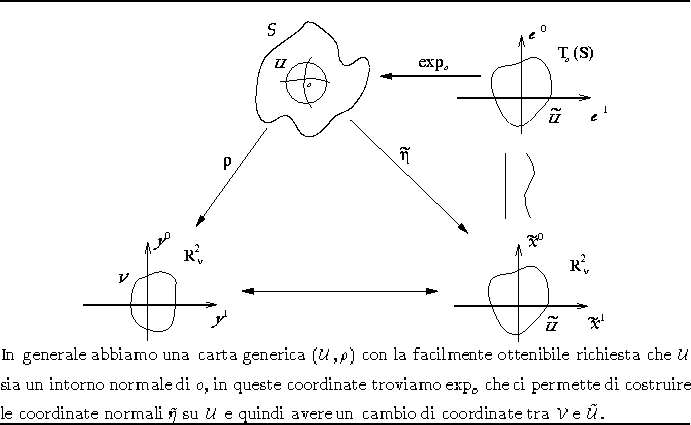
Figura 1.2: Coordinate normali su S.
Della seguente proposizione riportiamo anche la dimostrazione dato che è fondamentale per sviluppare alcuni metodi di diagonalizzazione.
Proposizione
1.16
Sia S varietà differenziale bidimensionale, ![]() la sua
metrica, o un punto di S, allora per ogni intorno normale
la sua
metrica, o un punto di S, allora per ogni intorno normale
![]() di o esistono delle coordinate
di o esistono delle coordinate ![]() tali
che soddisfano:
tali
che soddisfano:
Le coordinate 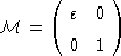
![]() .
.
![]() costruite nella dimostrazione
sono dette coordinate normali.
costruite nella dimostrazione
sono dette coordinate normali.
Dimostrazione
Sia ![]() una base ortonormale per
una base ortonormale per ![]() , sia
, sia
![]() la relativa base duale canonica. Consideriamo
la relativa base duale canonica. Consideriamo

e pongo
![]()
Dato che per la proposizione 1.13 ![]() è un
diffeomorfismo, le
è un
diffeomorfismo, le ![]() sono ben definite e
sono ben definite e ![]() è una carta per
S.
è una carta per
S.
Se ![]() vale
vale ![]() , tenendo conto
dell'osservazione 1.12 possiamo scrivere:
, tenendo conto
dell'osservazione 1.12 possiamo scrivere:
![]()
e dunque
![]()
Prendendo ![]()
![]() si ottiene
si ottiene ![]() e quindi vale la (i). A questo
punto l'equazione delle geodetiche data dalla definizione 1.1
si riduce a
e quindi vale la (i). A questo
punto l'equazione delle geodetiche data dalla definizione 1.1
si riduce a
![]()
ed in particolare:
![]()
che implica sia verificata la (ii).
![]()
Esempio
1.17
Nell'esempio 1.7 abbiamo visto che la geodetica con velocità
iniziale .
![]() è la retta
è la retta ![]() e quindi
e quindi
![]()
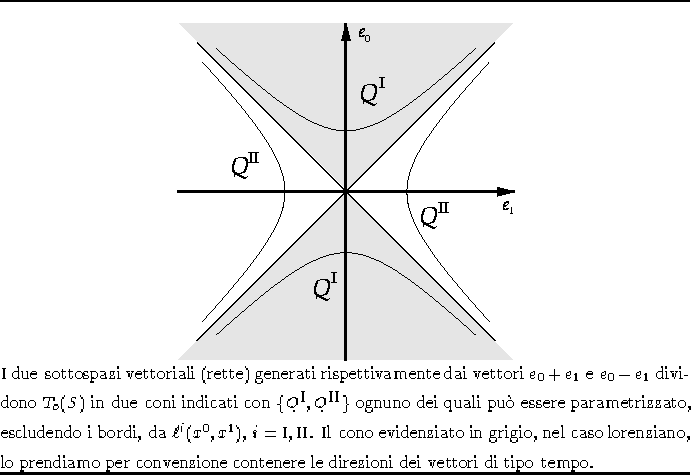
Figura 1.3: Coordinate Iperboliche su ![]()
Proposizione
1.18
Con riferimento alla figura 1.3, se
===
===
definiscono nel caso lorenziano una parametrizzazione dei punti dei coni
mentre nel caso riemanniano
===
===
con ![]() , ed
, ed
![]() è una base ortonormale di
è una base ortonormale di ![]() ,
,
![]() scelto a piacere, le funzioni definite (funzione
definita) come
scelto a piacere, le funzioni definite (funzione
definita) come
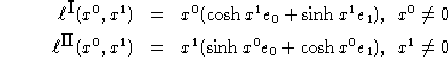
![]()
![]() ,
, ![]() delimitati dalle rette (escluse):
delimitati dalle rette (escluse):
![]()
![]() è una parametrizzazione dei punti del
piano
è una parametrizzazione dei punti del
piano ![]() con esclusione del punto 0. Inoltre, fissato un certo
con esclusione del punto 0. Inoltre, fissato un certo
![]() le funzioni appena definite risultano invertibili su:
le funzioni appena definite risultano invertibili su:
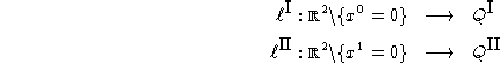
![]()
![]() la semiretta dei numeri reali
positivi non nulli e
la semiretta dei numeri reali
positivi non nulli e ![]() la semiretta dei numeri reali negativi, 0
compreso.
la semiretta dei numeri reali negativi, 0
compreso.
Dimostrazione
Il caso riemanniano è elementare, essendo le coordinate date da ![]() le
ben conosciute coordinate polari del piano. Per il caso lorenziano
dobbiamo far vedere che
le
ben conosciute coordinate polari del piano. Per il caso lorenziano
dobbiamo far vedere che ![]() ,
, ![]() è una
parametrizzazione dei punti dell'i-esimo cono escludendo le rette:
è una
parametrizzazione dei punti dell'i-esimo cono escludendo le rette:
![]()
che nel caso lorenziano sono i sottospazi vettoriali di ![]() contenenti i vettori di tipo nullo. Analizziamo solo il caso che ci
interessa maggiormente, il caso del cono costituito dai vettori di tipo
tempo, ovvero il cono di colore grigio indicato con I in figura
1.3, il caso del cono
contenenti i vettori di tipo nullo. Analizziamo solo il caso che ci
interessa maggiormente, il caso del cono costituito dai vettori di tipo
tempo, ovvero il cono di colore grigio indicato con I in figura
1.3, il caso del cono ![]() è perfettamente analogo.
è perfettamente analogo.
Dalla definizione si vede che ![]() è sicuramente continua e di
classe
è sicuramente continua e di
classe ![]() su tutto
su tutto ![]()
![]() , dobbiamo solo mostrare che
, dobbiamo solo mostrare che ![]() all'interno del cono
all'interno del cono ![]() è
invertibile. Per far questo prendiamo un vettore
è
invertibile. Per far questo prendiamo un vettore ![]() contenuto in
contenuto in ![]() e mostriamo che esiste un'unica coppia
e mostriamo che esiste un'unica coppia
![]()
per cui vale
Se vogliamo che la 1.2 sia verificata si deve avere:
![]()
Quindi ricavando ![]() si ottiene
si ottiene
![]()
Se v sta nel cono ![]() si deve avere che
si deve avere che ![]() e quindi
l'espressione che dà
e quindi
l'espressione che dà ![]() è ben definita e di classe
è ben definita e di classe ![]() su tutto
il cono
su tutto
il cono ![]() . Per quanto riguarda
. Per quanto riguarda ![]() si deve avere:
si deve avere:
![]()
e dunque, tenendo conto che ![]() , e che
, e che ![]() ha lo
stesso segno di
ha lo
stesso segno di ![]()
![]() viene:
viene:
![]()
che è ![]() sul cono
sul cono ![]() .
.
![]()
Ora abbiamo gli strumenti necessari per dare la seguente definizione:
Definizione
1.19
Sia
===
===
Chiameremo ![]() una base ortonormale di
una base ortonormale di ![]() , o un punto
scelto a piacere di S, allora le mappature geodetiche iperboliche
(mappatura geodetica polare) sono le funzioni (funzione):
, o un punto
scelto a piacere di S, allora le mappature geodetiche iperboliche
(mappatura geodetica polare) sono le funzioni (funzione):
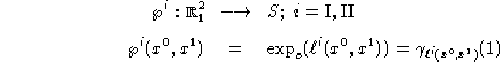
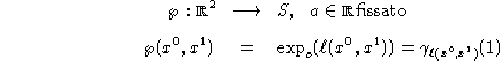
![]() mappatura geodetica iperbolica temporale,
mappatura geodetica iperbolica temporale,
![]() mappatura geodetica iperbolica spaziale e
mappatura geodetica iperbolica spaziale e ![]() mappatura geodetica polare.
mappatura geodetica polare.
Osservazione 1.20 Notare che l'osservazione 1.12 applicata alla precedente definizione ci dice
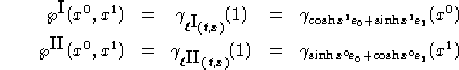
===
![]()
=== e dunque tenendo presente che in 0 la metrica di S è pari a quella lorenziana (euclidea) canonica e che l'accelerazione di una geodetica è nulla, si ha:
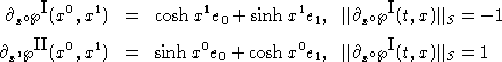
===
![]()
===

Figura 1.4: Coordinate Iperboliche temporali su S.
Proposizione
1.21
Se
===
===
allora le mappature geodetiche della definizione 1.19 sono
dei diffeomorfismi se ristrette a:
===
===
![]() è un intorno normale del punto o di S, poniamo, con
riferimento alla figura 1.4:
è un intorno normale del punto o di S, poniamo, con
riferimento alla figura 1.4:
![]()

![]()
![]()
Dimostrazione
Scelto ![]() intorno normale di o in S,
la proposizione 1.13 ci da che
intorno normale di o in S,
la proposizione 1.13 ci da che ![]() è un
diffeomorfismo tra un intorno
è un
diffeomorfismo tra un intorno ![]() di 0 in
di 0 in ![]() e un
intorno
e un
intorno ![]() di o in S. La proposizione 1.16
afferma che scelto
di o in S. La proposizione 1.16
afferma che scelto ![]() esistono delle coordinate su
esistono delle coordinate su ![]() che producono una base ortonormale in
che producono una base ortonormale in ![]() e quindi si può
applicare la proposizione 1.18. Da quest'ultima otteniamo
in particolare che che
e quindi si può
applicare la proposizione 1.18. Da quest'ultima otteniamo
in particolare che che ![]() (analogo discorso vale per
(analogo discorso vale per ![]() )
è un diffeomorfismo tra
)
è un diffeomorfismo tra ![]() e il cono
e il cono ![]() (bordi
esclusi) di figura 1.3 e dunque
(bordi
esclusi) di figura 1.3 e dunque ![]() ,
restringendo
,
restringendo ![]() a
a ![]() e
e ![]() a
a ![]() ,
risulta composizione di diffeomorfismi, ed è a sua volta un
diffeomorfismo tra:
,
risulta composizione di diffeomorfismi, ed è a sua volta un
diffeomorfismo tra:
![]()
Infine se ![]() è un diffeomorfismo lo sarà anche la sua inversa
è un diffeomorfismo lo sarà anche la sua inversa
![]() e
e ![]() risulta essere una carta per S. c.v.d.
risulta essere una carta per S. c.v.d.
Il caso riemanniano è del tutto simile.
![]()
Proposizione
1.22
La metrica riscritta secondo le coordinate prodotte dalla mappatura geodetica
lorenziane
mentre con
![]() ed euclidea
ed euclidea ![]() è della forma:
è della forma:
![]()
![]() è della forma:
è della forma:
![]()
Dimostrazione
Dimostriamolo per ![]() , il secondo caso lorenziano e il caso
riemanniano sono perfettamente analoghi.
, il secondo caso lorenziano e il caso
riemanniano sono perfettamente analoghi.
La situazione in cui ci troviamo è quella riportata in figura
1.4. Calcoliamo E tenendo conto dell'osservazione
1.20 e che le curve a ![]() costante sono le geodetiche:
costante sono le geodetiche:
![]()
e vale anche sempre per l'osservazione 1.20:
![]()
Calcoliamo F
![]()
quindi F è costante lungo le geodetiche. Inoltre ![]() è
costantemente 0, in particolare
è
costantemente 0, in particolare ![]() è 0 e dunque dato
che come funzione F è definita su tutto
è 0 e dunque dato
che come funzione F è definita su tutto ![]() :
:
![]()
e dato che lungo le geodetiche è costante F risulterà nulla su tutto
![]() .
.
Dato che non abbiamo fatto altro che un cambio di coordinate, la metrica dovrà essere ancora non singolare ed avere lo stesso indice, quindi deve essere:
![]()
![]()
Nel caso lorenziano non troviamo un vero e proprio intorno di o in cui
la metrica è definita ed in forma diagonale, ma piuttosto troviamo dei coni
con origine o che si sviluppano nel tempo o nello spazio. Se
vogliamo avere, ad esempio, un intorno di o che si sviluppi nel
tempo, ci basta prendere un intorno normale ![]() di o e un
punto
di o e un
punto ![]() che stia su una qualsiasi geodetica di tipo tempo
passante per o e trovo le coordinate iperboliche centrate su p, in
questo modo
che stia su una qualsiasi geodetica di tipo tempo
passante per o e trovo le coordinate iperboliche centrate su p, in
questo modo ![]() conterrà o e cosìho trovato l'intorno cercato.
conterrà o e cosìho trovato l'intorno cercato.
L'unico problema per calcolare effettivamente le mappature geodetiche sta
nel trovare le geodetiche passanti per P. Questo problema e' difficile
da risolvere, ma numericamente dà origine a sistemi di
equazioni differenziali ordinarie che si sanno trattare e quindi non dà
problemi ottenere una approssimazione numerica di ![]() .
.