1.2.2 Coordinate ortogonali via integrali primi.

Illustriamo, adattandolo alla notazione di questa tesi, il metodo per ottenere coordinate ortogonali usato su [&make_named_href('', "node19.html#doc","[DC]")] a pg. 175 e seguenti che produce risultati che abbiamo già raggiunto ma che non richiede di conoscere le geodetiche di S. Questo metodo si applica ugualmente sia al caso lorenziano che a quello riemanniano.

Definizione  1.23 Una curva è una curva integrale per se , ovvero per ogni .

Dal teorema di esistenza ed unicità delle soluzioni per equazioni ordinarie differenziali, a riguardo cfr. per esempio [&make_named_href('', "node19.html#hur","[HR]")], otteniamo la seguente:

Proposizione  1.24   Se allora per ogni esiste un intervallo intorno a 0 ed un'unica curva integrale

con , .

Osservazione  1.25 Notare che di può traslare a piacere I in , se è curva integrale per W, anche la curva

con costante, è una curva integrale per W.

Corollario  1.26 Se sono curve integrali per tali che per , allora .

Teorema  1.27   Sia S una varietà differenziale, una sua carta, allora per ogni esiste un intorno di p, un intervallo ed una funzione

tale che

1. Fissato la curva , è una curva integrale di W passante per q con .
2. è differenziabile.

è detto flusso di W in .

Dimostrazione cfr. [&make_named_href('', "node19.html#doc","[DC]")] pg. 176, [&make_named_href('', "node19.html#hur","[HR]")] cap. 2.

 
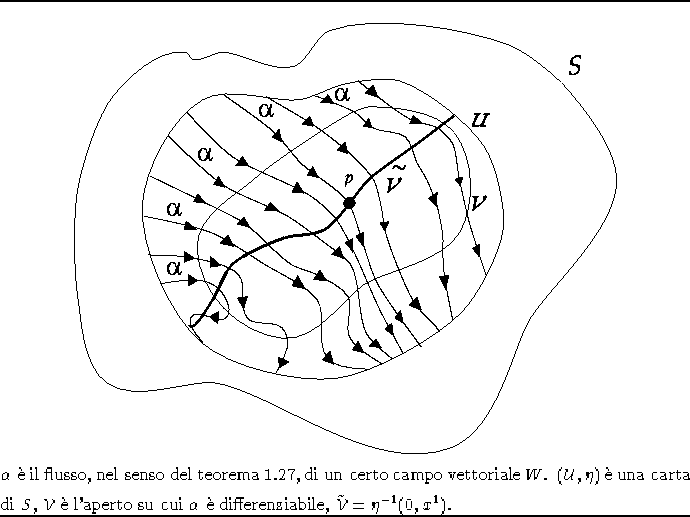
Figura 1.5: Flusso di un campo vettoriale W. 

Teorema  1.28  

Sia W un campo vettoriale di , una carta di S, p un punto di S, , allora esiste un intorno di p e una funzione differenziabile

tale che f è costante lungo le linee integrali di W e per ogni . f viene detta integrale primo locale di W.

Dimostrazione Scegliamo delle coordinate di tali che e . Sia

il flusso di W locale a p dato dal teorema 1.27. Poniamo, cfr. fig. 1.5,

e sia la restrizione di a . Si avrà che

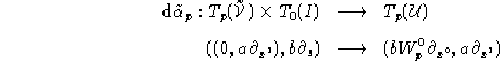
e quindi è non singolare, quindi si può applicare il teorema della funzione inversa ottenendo l'inversa definita e differenziabile su un intorno di p.

Tenendo conto che e chiamando con

le proiezioni canoniche, abbiamo che la funzione f definita come

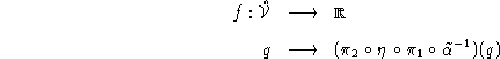
è ben definita. Fissando , se è una curva integrale per W, esisteranno unici, per la proposizione 1.24 e per la bieettività di , , e con e varrà . Calcolando f su otterremo:

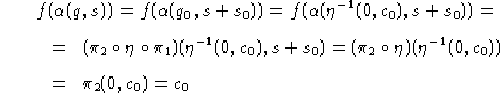
quindi dato che per ogni , fissato, f risulta costante lungo le curve integrali di W contenute in . Inoltre dato che è non singolare, eventualmente rimpicciolendo , abbiamo che per ogni .

Teorema  1.29  

Sia una carta per S, , un punto in cui e risultano linearmente indipendenti, allora esiste un intorno di p e delle coordinate tali che:

Dimostrazione Sia l'intorno di p dove l'integrali primi di, rispettivamente, , sono definiti. Definiamo la mappa:

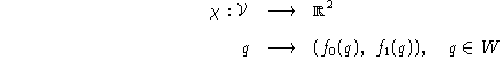
Per definizione è costante sulle curve integrali di e , abbiamo che in p vale:

dove dato che e sono linearmente indipendenti in p. Analogamente

con . Ne consegue che è non singolare e è un diffeomorfismo locale. Esisterà un intorno di diffeomorfo a un intorno di p; ponendo si ha che la coppia è una carta per S, , che soddisfa le ipotesi.

Teorema  1.30  

Per ogni esiste una carta , tale che la matrice della metrica nelle nuove coordinate risulta in forma diagonale. sono dette Coordinate Ortogonali.

Dimostrazione Consideriamo un carta arbitraria , contenente il punto o. Sia la matrice della metrica in queste coordinate:

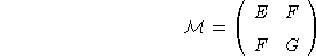
Allora, se definiamo due campi vettoriali su come

è subito verificato che questi 2 campi sono perpendicolari per ogni . Nel caso riemanniano sono ben definiti su tutto mentre nel caso lorenziano dobbiamo richiedere che E sia diverso da zero in cosìche possiamo avere tutto un intorno di o in cui sia E sia diverso da zero e quindi, eventualmente restringendo , possiamo ancora definire su e quindi applicare il teorema precedente 1.29 in ogni punto p di trovando la carta cercata.

Se E è nullo su tutto ma G è diverso da 0 in o, eventualmente restingendo , possiamo definire

che saranno vettori non nulli e perpendicolari su tutto e quindi possiamo di nuovo applicare il teorema precedente trovando la carta cercata.

Infine se E e G sono identicamente nulli su tutto definiamo:

che risulterà ancora un campo perpendicolare su e non nullo e di nuovo potremo applicare il teorema prcedente ottenendo la la tesi.