


Next: Applicazione funzioni 1
Up: 3 Implementazione
Previous: 3 Implementazione
Descriviamo l'utilizzo delle funzioni contenute nel pachetto NImmersion.m.
Per esempi guardare nel disco in allegato. Il codice Mathematica
è riportato usando i Font Courier.
Il parametro indicato opts, dove presente, rappresenta le opzioni supportate
dalla funzione ed è facoltativo.
- ND[data,h,opts]
- Calcola la derivata numerica di una
funzione. La funzione è data come una sequenza di valori in
 assunti in punti
successivi ognuno dei quali distante di h dal precedente.
Le opzioni supportate sono:
assunti in punti
successivi ognuno dei quali distante di h dal precedente.
Le opzioni supportate sono:
- ND[data,opts]
- Come la precedente solo che la
funzione da derivare è data come una sequenza di coppie
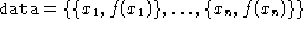 .
.
- MakeData[f,x,{xmin,xmax},opts]
- Restituisce una approssimazione
numerica di f nell'intevallo
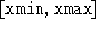 nella forma richiesta
dalla funzione ND[data]. Opzioni supportate:
nella forma richiesta
dalla funzione ND[data]. Opzioni supportate:
- HaccaK1[t,cet,cct,k1]
- Calcola la funzione
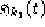 (cfr. sez.
2.1 per una metrica decomponibile
di componenti
(cfr. sez.
2.1 per una metrica decomponibile
di componenti 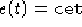 ,
, 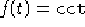 .
.
- OptimizeDelta[f,x,{xmin,xmax},maxinc,opts]
- Restituisce una coppia di valori
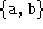 , a è il numero di punti in cui suddividere l'intervallo
, a è il numero di punti in cui suddividere l'intervallo
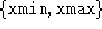 affinchè la funzione f[x] abbia un incremento inferiore a
maxinc quando x varia meno di b.
Opzioni supportate:
affinchè la funzione f[x] abbia un incremento inferiore a
maxinc quando x varia meno di b.
Opzioni supportate:
- ImmersionDecomponible[cet, ccx, cct,{t, x},{a,b},sur,fbb,opts]
-
Restituisce l'immersione
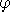 di una metrica decomponibile di componenti
di una metrica decomponibile di componenti
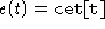 ,
, 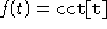 ,
, 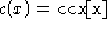 con le
condizioni iniziali
con le
condizioni iniziali 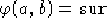 e
e 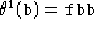 .
.
Opzioni supportate:
- ListIntegrate2[data, h, k]
- Calcola l'integrale di
un funzione f data come una lista di valori
 assunti dalla funzione f su una
successione di punti distanti di h l'uno dall'altro. Il risultato è
restitutito come una lista di valori assunti dall'integrale di f su punti
distanti h l'uno dall'altro. L'integrale calcolato nel primo punto è
sempre nullo. L'integrazione è eseguita interpolando con polinomi di grado
k i dati data in ingresso.
assunti dalla funzione f su una
successione di punti distanti di h l'uno dall'altro. Il risultato è
restitutito come una lista di valori assunti dall'integrale di f su punti
distanti h l'uno dall'altro. L'integrale calcolato nel primo punto è
sempre nullo. L'integrazione è eseguita interpolando con polinomi di grado
k i dati data in ingresso.
- ListIntegrate2[data, k]
- Analoga alla funzione precedente, con
la differenza che la funzione f da integrare è data come una lista di coppie
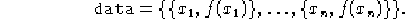
Restituisce l'integrale nella
stessa forma.
- EFGComponents[sur,t,x,ep]
- Calcola le componenti della metrica della superfice
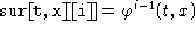 per i=1,2,3. Restituisce una lista
di tre elementi
contenente le componenti E,F,G. ep è
per i=1,2,3. Restituisce una lista
di tre elementi
contenente le componenti E,F,G. ep è  .
.
- Kurvature[e,g,{t,x},ep]
- Calcola la curvatura della metrica
diagonale con
 ,
, 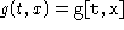 ,
, 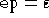 .
.
- ColorStretched[v,s]
- Restituisce una direttiva grafica di colore dipendente da v.
s regola l'associazione colore-valore.
v e s può variare nell'intevallo chiuso
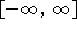 .
.
- PlotLegend[vmin,vmax,off,s,npoints]
- Disegna come varia il colore
dato dalla funzione ColorStretched[v,s] per
 che varia tra
vmin e vmax. npoints è la risoluzione usata.
che varia tra
vmin e vmax. npoints è la risoluzione usata.
- InverseCosSin[a,b]
- a e b sono due liste di
elementi
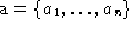 e
e
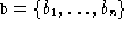 che rappresentano l'approssimazione
numerica di due funzioni a(y) e b(y) continue. La funzione
InverseCosSin[a,b] restituisce una lista
che rappresentano l'approssimazione
numerica di due funzioni a(y) e b(y) continue. La funzione
InverseCosSin[a,b] restituisce una lista
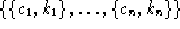 con la proprietà che
con la proprietà che 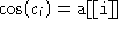 e
e  e la differenza
e la differenza 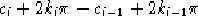 è minima tra
tutte le possibili con
è minima tra
tutte le possibili con 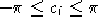 .
.
- ConstrainAngle2[a,p]
- Prende l'angolo a e restituisce
una coppia
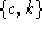 con
con 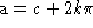 e
e 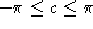 . p è la precisione
con cui effettuare i calcoli.
. p è la precisione
con cui effettuare i calcoli.
- ConstrainAngle1[a,p]
- Prende l'angolo a e restituisce
un un numero
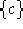 con
con  un multiplo di
un multiplo di 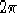 e
e 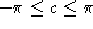 . p è la precisione con cui effettuare i calcoli.
. p è la precisione con cui effettuare i calcoli.
- ParametricListPlot3D[sur1,sur2,sur3,opts]
-
sur1, sur2, sur3 sono delle matrici che rappresentano
l'approssimazione numerica di una funzione
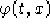 calcolata su una
griglia
calcolata su una
griglia 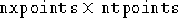 . opts sono le opzioni di
Graphics3D che si vuole abbia la grafica generata.
. opts sono le opzioni di
Graphics3D che si vuole abbia la grafica generata.
- ParametricListPlot3D[sur1,sur2,sur3,col,opts]
-
Come la funzione precedente solo è possibile specificare un matrice aggiuntiva col
contenente una serie di primitive grafiche da associare ad ogni poligono
disegnato.
- ThetaInit[ep,g,{t,tmin,tmax},{x,xmin,xmax},opts]
-
Calcola le condizioni iniziali per applicare l'algoritmo per il caso
generale.
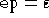 ,
, 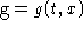 . Si assume
. Si assume 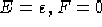 .
Opzioni supportate:
.
Opzioni supportate:
- thetax[th0,th2,th1t,th2t,gt,g,ep]
- Resituisce una lista
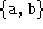 con
con 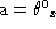 ,
, 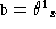 calcolati a
calcolati a
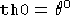 ,
,  ,
, 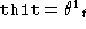 ,
, 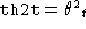 ,
,
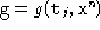 ,
, 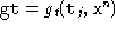 ,
,
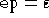 .
.
- RVector[th0,th1,ep]
- I parametri hanno lo stesso significato
della funzione precedente. Viene restituita una lista di tre elementi
contenenti le componenti del vettor R.
- VVector[th0,th1,th2,ep]
- Come la precedente funzione, solo che
viene restituito il vettore V.
- ImmersionOf[g,{t,tmin,tmax},{x,xmin,xmax},th,ng,delta,ep,opts]
-
I parametri in ingresso di questa funzione sono
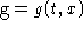 , gli intervalli
in cui varia t e x,
, gli intervalli
in cui varia t e x, 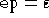 , e le opzioni facoltative opts. Il resto dei parametri
devono essere dei simboli a cui verranno assegnati i risultati.
th sarà un lista di tre matrici
, e le opzioni facoltative opts. Il resto dei parametri
devono essere dei simboli a cui verranno assegnati i risultati.
th sarà un lista di tre matrici 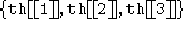 che rappresentano
la soluzione numerica ai sistemi 2.22, 2.23 dopo aver applicato l'algoritmo
illustrato nella sezione 1.4. ng conterrà la matrice rappresentante l'approssimazione
numerica effettuata sulla griglia della componente g(t,x) delle metrica, delta è una lista di 2
elementi
che rappresentano
la soluzione numerica ai sistemi 2.22, 2.23 dopo aver applicato l'algoritmo
illustrato nella sezione 1.4. ng conterrà la matrice rappresentante l'approssimazione
numerica effettuata sulla griglia della componente g(t,x) delle metrica, delta è una lista di 2
elementi 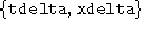 che prenderanno il valore, rispettivamente, della
distanza di due punti della griglia
lungo t e lungo x.
Opzioni supportate:
che prenderanno il valore, rispettivamente, della
distanza di due punti della griglia
lungo t e lungo x.
Opzioni supportate:
- ImmersedSurface[th,ng,{tdelta,xdelta},ep,k,sur,opts]
-
I parametri th,ng, tdelta, xdelta sono i risultati della funzione ImmersionOf[],
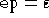 , k è il parametro da passare alla funzione ListIntegrate2 indicante
il grado dei polinomi da utilizzare nell'interpolazione della funzione da integrare. sur
è un simbolo a cui verrà assegnato il risultato consistente in una lista di tre matrici
, k è il parametro da passare alla funzione ListIntegrate2 indicante
il grado dei polinomi da utilizzare nell'interpolazione della funzione da integrare. sur
è un simbolo a cui verrà assegnato il risultato consistente in una lista di tre matrici
 rappresentanti un'approssimazione numerica dell'integrale
1.6, pg.
rappresentanti un'approssimazione numerica dell'integrale
1.6, pg. 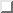 del Teorema di Equivalenza, ovvero una rappresentazione numerica della superfice
con metrica
del Teorema di Equivalenza, ovvero una rappresentazione numerica della superfice
con metrica 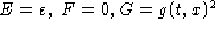 . Le opzioni supportate sono le stesse della funzione precedente.
. Le opzioni supportate sono le stesse della funzione precedente.
- PlotImmersionError[sur1,sur2,sur3,ng,ep,{tdelta,xdelta},opts]
-
sur1, sur2, sur3 sono le componenti della lista sur restituita dalla precedente
funzione, tdelta, xdelta , ep, ng hanno lo stesso significato della funzione precedente,
e sono restituiti da essa.
opts sono le opzioni di Graphics3D che vogliamo abbia la grafica prodotta.
Questa funzione disegna tre superfici che indicano la differenza tra le componenti della
metrica della superfice approssimata da sur e le componenti della metrica che si vuole immergere.
- ImmergiEdisegna[ep,g,{t,tmin,tmax},ntpoints,{x,xmin,xmax},nxpoints,k,
-
nome]
Esempio di utilizzo delle funzioni presenti in questo pacchetto per rappresentare una
superfice di metrica
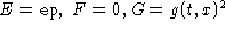 colorandola in base alla curvatura.
Viene anche disegnata una leggenda che indica il legame curvatura-colore e tre superfici
rappresentanti l'errore nelle 3 componenti. nome è
il nome del file in cui salvare, come primitive
Graphics3D[], la superfice sup generata, la legenda leg
dei colori per la curvatura, il disegno dell'errore err[[1]] su E ,
l'errore err[[2]] su F e l'errore err[[3]] su G,
l'espressione simbolica di
colorandola in base alla curvatura.
Viene anche disegnata una leggenda che indica il legame curvatura-colore e tre superfici
rappresentanti l'errore nelle 3 componenti. nome è
il nome del file in cui salvare, come primitive
Graphics3D[], la superfice sup generata, la legenda leg
dei colori per la curvatura, il disegno dell'errore err[[1]] su E ,
l'errore err[[2]] su F e l'errore err[[3]] su G,
l'espressione simbolica di 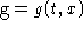 e il valore di
k, xmin, xmax, tmin, tmax.
e il valore di
k, xmin, xmax, tmin, tmax.
- ImmergiEdisegnaBatch[ep,g,{t,tmin,tmax},ntpoints,{x,xmin,xmax},nxpoints,k,
-
nome]
Come la funzione precedente, solo che la grafica invece che essere
visualizzata viene salvata su disco sia in formato postscript sia in
formato RPL.
Sul disco è contenuto anche il pacchetto RPLScript.m che abbiamo
sviluppato basandoci sul pacchetto TreeScript.m della versione 2.03
di Mathematica. Definisce la funzione RPLScript[nome,grs] che prende
una primitiva grafica grs di tipo Graphics3D[] e salva in
nome un oggetto descritto in linguaggio RPL (cfr. [&make_named_href('',
"node19.html#rpl","[RPL]")]) adatto
ad essere letto dal programma Real3D . Una versione demo per il
sistema operativo AmigaDOS, utilizzata per creare alcune animazioni del
disco in allegato, è prelevabile da uno qualsiasi dei nodi aminet (in
italia Go Aminet Server. Oltre al
notebook t1.m di esempio di uso delle funzioni di Nimmersion.m
è presente anche un notebook Equazioni.m che contiene, in codice
mathematica, tutto il procedimento illustrato nel capitolo 1 e 2 di questa
tesi. Si consiglia comunque di guardare nel disco in allegato il file
ReadMe.txt per un'elenco più dettagliata di ulteriori programmi
di utilità ivi contenuti e sviluppati per realizzare questa tesi.
Download RPLScript.ma
. Una versione demo per il
sistema operativo AmigaDOS, utilizzata per creare alcune animazioni del
disco in allegato, è prelevabile da uno qualsiasi dei nodi aminet (in
italia Go Aminet Server. Oltre al
notebook t1.m di esempio di uso delle funzioni di Nimmersion.m
è presente anche un notebook Equazioni.m che contiene, in codice
mathematica, tutto il procedimento illustrato nel capitolo 1 e 2 di questa
tesi. Si consiglia comunque di guardare nel disco in allegato il file
ReadMe.txt per un'elenco più dettagliata di ulteriori programmi
di utilità ivi contenuti e sviluppati per realizzare questa tesi.
Download RPLScript.ma



Next: Applicazione funzioni 1
Up: 3 Implementazione
Previous: 3 Implementazione
Charlie &
Tue Sep 24 00:18:57 PDT 1996
![]()